Ребро - тетраэдр
Cтраница 2
Пусть ребро АВ тетраэдра ABCD равно ребру А В тетраэдра A B C D и трехгранные углы при вершинах А и В первого тетраэдра оба равны или оба симметричны соответственно трехгранным углам при вершинах А и В второго. Так как равные элементы обоих тетраэдров располагаются, по условию, в одном и том же порядке, то общий двугранный угол при ребре АВ двугранных углов при вершинах А и В будет равен двугранному углу при ребре А В. Оба тетраэдра будут опять равны или симметричны по первому признаку, рассмотренному выше. [16]
Два ребра тетраэдра перпендикулярны скрещивающимся с ними ребрам. Доказать, что и два других скрещивающихся ребра тетраэдра перпендикулярны. [17]
Два ребра тетраэдра перпендикулярны скрещивающимся с ними ребрам. Доказать, что и два других скрещивающихся ребра тетраэдра перпендикулярны. [18]
Два ребра тетраэдра перпендикулярны скрещивающимся с ними ребрам. Доказать, что и два других скрещивающихся ребра тетраэдр а-перпендикулярны. [19]
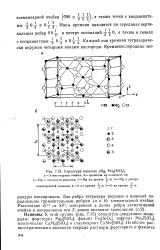 |
Структура оливина ( Mg, Fe2 [ SiO4 ]. [20] |
Два ребра тетраэдра ( верхнее и нижнее) параллельны горизонтальным ребрам ( а и Ь) элементарной ячейки. [21]
Шесть ребер тетраэдра разделены в данных отношениях. Найти отношение объема выпуклого многогранника ( октаэдра), вершинами которого служат эти точки деления, к объему тетраэдра. [22]
Два ребра тетраэдра перпендикулярны скрещивающимся с ними ребрам. Доказать, что и два других скрещивающихся ребра тетраэдра перпендикулярны. [23]
Длину ребра тетраэдра обозначим а. Опустим перпендикуляр DO на плоскость ABC. Прямая АО является проекцией прямой AD на плоскость ABC, значит, угол между прямой AD и этой плоскостью равен ОАО. [24]
Два ребра тетраэдра перпендикулярны скрещивающимся с ними ребрам. Доказать, что и два других скрещивающихся ребра тетраэдра перпендикулярны. [25]
Длина ребра тетраэдра равна а. [26]
Длину ребра тетраэдра обозначим а. Опустим перпендикуляр DO на плоскость ЛВС. [27]
На ребрах тетраэдра ( рис. 20.1, а) находятся точки а, Ь, с, которые характеризуют растворы, насыщенные одним из компонентов, а на гранях - изотермы соответствующих тройных систем. Точки Е, EZ и Es - эвтонические, а точка Е - тройная эвтоника. Фигуративные точки на кривых EEi, EEZ и ЕЕ3 отвечают растворам, насыщенным двумя компонентами в присутствии третьего. Объемы кристаллизации каждого компонента образуются лучами, проведенными из точек состава твердых фаз. [28]
Через каждое ребро тетраэдра проведена плоскость, параллельная противоположному ребру. [29]
 |
Тетраэдрический дефект упаковки, перерезанный дислокацией с вектором герса АС. [30] |
Страницы: 1 2 3 4