Никакое ребро

Cтраница 1

Никакое ребро Е0 ( о, 60) в G не может быть ациклическим, так как существует ориентированная простая цепь Q ( bo, UQ), которая вместе с Z. [1]

Никакое ребро не может повторяться. [2]

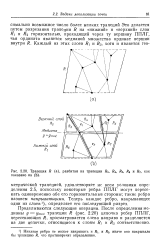Трапеция R ( а, разбитая на трапеции Rs, Rt, Rs, Re и Rj, как показано на ( b. [3]

Никакое ребро не может накрывать и Я, и R2, иначе оно накрывало бы трапецию R, что противоречит определению. [4]

Никакое ребро в B ( L) не может быть излишним, так как иначе оно приводило бы к уменьшению В. В В существует только одно ребро, соединяющее пару листовых множеств LI и L2 в G ( и в В), так как если одно такое ребро содержится в В, то другие, очевидно, являются излишними. Ребра из В образуют порождающий граф для G, и никакие ребра из В не могут быть излишними, так как это снова приводило бы к уменьшению В. [5]

Никакое ребро пе может повторяться. [6]

Вершина, не инцидентная никакому ребру, называется изолированной. [7]

Вершина, не инцидентная никакому ребру, называется изолированной. При определении множества вершин V данного графа часто имеет смысл учитывать только неизолированные вершины. [8]

Вершина, не инцидентная никакому ребру, называется изолированной. Ребро, соединяющее вершину саму с собой, называется петлей. [9]

Вершина, не принадлежащая никакому ребру графа. Примером может служить запись-член сингулярного набора в модели данных КОДАСИЛ. [10]

Точка, которая не ограничивает никакого ребра, не связана ни с одним ребром и, следовательно, вообще ни с каким другим элементом в смысле условия II. Таким образом, она должна в силу этого условия составлять самостоятельный граф. [11]

Внутренние вершины Я, не инцидентные никаким ребрам из Я. [12]

Графы переходов автоматов, допускающие языки, представленные регулярными выражениями ( a P V. ( б Рт. ( e Р. [13]

Наконец, из sf, очевидно, никакие ребра не выходят. [14]

Береговая насосная станция с последовательно работающими насосами. [15]

Страницы: 1 2 3 4