Разделяющее ребро

Cтраница 2

Теорема 5.2.1. Конечный граф с четными локальными степенями не может иметь разделяющих ребер. [16]

Кривая коэффициента kCs скорости у фланца всасывающего колена. [17]

Как видно из рис. 97, в верхней части всасывающего патрубка имеется разделяющее ребро, для того чтобы отвести поток и не дать жидкости вращаться до входа в рабочее колесо. [18]

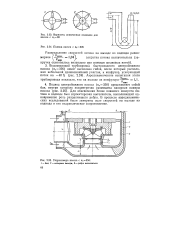Варианты испытанных подводов для насоса с ns 80.| Подвод насоса с п 326.| Гидрокамера насоса с ns350. [19]

Для обеспечения более плавного поворота потока в подводе был спроектирован вытеснитель, выполняющий одновременно роль разделяющего ребра. В процессе аэродинамических исследований были замерены поле скоростей на выходе из подвода и его гидравлическое сопротивление. [20]

Всасывающий подвод ГЦН с 326.| Гидрокамера центробежного насоса ( / гвх2 6 / 0. a f l ( 2H - й и / 3 - 0. eQ 7D0. r0 3lD0. [21]

Для обеспечения более плавного поворота потока в подводе предусматривается вытеснитель 3, выполняющий одновременно роль разделяющего ребра. В процессе аэродинамических исследований были измерены поле скоростей на выходе из подвода и его гидравлическое сопротивление. Поле скоростей без вытеснителя более симметрично. [22]

Доказать, что условие теоремы 14.4.1 также п достаточно для того, чтобы Е было разделяющим ребром. [23]

Аналогично доказательству теоремы 16 за тем лишь исключением, что разделяющему ( внешнее удаление вершины) множеству вершин в S взаимно однозначно соответствует множество разделяющих ребер в графе WS - ( X, R), который получается из вторичной сети WS ( X, R) гиперсети S отождествлением вершин, инцидентных такому ребру г, для которого не существует слабо инцидентных вершин из X. В этом случае в графе WS эти вершины будут отождествлены. [24]

Теорема 8.1.6. Неориентированный граф G0 является графом Gu бисвязного ориентированного графа G тогда и только тогда, когда граф G0 связен и не имеет разделяющих ребер. [25]

Подобные теоремы справедливы также для непересекающихся по ребрам простых цепей от А к В, если воспользоваться функцией дефицита, определенной по отношению к разделяющим ребрам. [26]

HI с некоторой другой компонентой У / 2, По тогда Е можно было бы добавить к 11 и при этом не получилось бы запрещенных частей (6.4.1), так как они не имеют разделяющих ребер. [27]

Аналогично, ребро а называется разделяющим вершины 8 и у в графе G, если р и у принадлежат одной компоненте связности и всякая цепь [ В, у ] содержит ребро а. Разделяющее ребро называют также перешейком. Каждый из концов любого перешейка, за исключением концевых вершин графа, является разделяющей вершиной. В дереве каждое ребро является перешейком, а каждая не концевая вершина разделяющей. [28]

Разделяющие ребра соответствуют в нашей интерпретации единственным мостам через реку или тупикам. Поэтому предположим, что в связном графе G0 нет разделяющих ребер. Можно построить бисвязные ориентированные части графа, вводя подходящие направления; например, из простого цикла возникают два таких графа. Эти ориентированные части графа образуют частично упорядоченное множество, если считать Н Н2, когда ребра Н2 принадлежат HI и имеют те же направления. [29]

Разделяющие ребра соответствуют в пашей интерпретации единственным мостам через реку или тупикам. Поэтому предположим, что в связном графе GO пет разделяющих ребер. Можно построить опсвязные ориентированные части графа, вводя подходящие направления; например, пз простого цикла возникают два таких графа. Эти ориентированные части графа образуют частично упорядоченное множество, если считать / / 1 э / / 2, когда ребра / / 2 принадлежат / / [ п имеют те же направления. Рассмотрим упорядоченное по включению семейство / / бисвя. [30]

Страницы: 1 2 3