Кратное ребро

Cтраница 3

Пусть G - граф без петель и кратных ребер и A ( G) - наибольшая из степеней его вершин. [31]

Взвешенный вариант этой теоремы легко получить, рассматривая кратные ребра. [32]

Граф с га помеченными вершинами без петель и кратных ребер полностью определяется множеством ребер. [33]

Если в графе вторичной сети WS имеется k кратных ребер между вершинами х, у и, кроме того, локальная связность вершин х, у в графе первичной сети PS не меньше k, то эти k кратных ребер можно реализовать по k независимым путям. [34]

Существует ли конечный граф ( без петель и кратных ребер), в котором нет двух вершин с одинаковыми степенями. [35]

В этой статье рассматриваются конечные неориентированные графы без кратных ребер и петель. Через E ( G) обозначено множество Вершин графа G, через K ( G) - множество его ребер. [36]

Пусть G и Н не имеют петель и кратных ребер, являются двухсвязными, содержат по 6 вершин и по 8 ребер. [37]

Построить однородный 9-вершинный граф ( без петель и кратных ребер), который не планарен вместе со своим дополнением. [38]

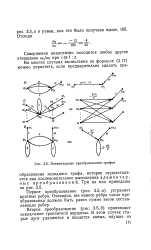Элементарные преобразования графов. [39]

Первое преобразование ( рис. 3.5, а) устраняет кратные ребра. Очевидно, вес нового ребра после преобразования должен быть равен сумме весов составляющих ребер. [40]

Ясно, что при этом легко представимы петли и кратные ребра. [41]

Пусть сеть Г является Н - разложимой сетью без кратных ребер. Достаточно ли для получения из нее неразложимой сети соединить каждую вершину v из ( Г) с одним из полюсов, с которыми v не смежна. [42]

Узловой граф четырех различных узлов. [43]

Сколько существует р-вершинных узловых графов, содержащих т пар кратных ребер. [44]

Теорема 2.5.4. В конечном графе G без петель и кратных ребер пусть / с есть длина длиннейшей простой цепи, а / о - максимальный индекс компонент по всем простым цепям. [45]

Страницы: 1 2 3 4