Значение - исходная величина
Cтраница 1
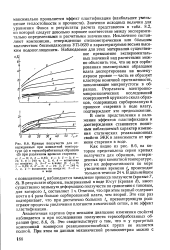 |
Кривые ползучести для от-вержденных при комнатной температуре ( а и термообработанных образцов ( б при различном времени старения. [1] |
Значения исходных величин для уравнения Фокса и результаты расчета представлены в табл. 8.2, из которой следует довольно хорошее соответствие между экспериментально определенными и расчетными значениями. Исключение составляют композиции, отвержденные стехиометрическим или большим; количеством бисимидазолина УП-0639 и характеризуемые весьма высоким водопоглощением. Наблюдаемое для этих материалов существенное превышение экспериментальных значений над расчетными можно объяснить тем, что не вся сорбированная полимерными образцами влага диспергирована на молекулярном уровне - часть ее образует кластеры конечной протяженности, заполняющие микропустоты в образцах. Результаты электронно-микроскопических исследований поверхностей хрупкого скола образцов, содержащих сорбированную в процессе старения в воде влагу, подтверждают это предположение. В свете представления о наложении эффектов пластификации и доотверждения становится понятным наблюдаемый характер изменения статических релаксационных свойств ЭКК в зависимости от времени старения в воде. [2]
Значения исходных величин ( л, р, k и др.) триняты такими же, как и в примере, иллюстрируемом фиг. [3]
Значения исходных величин задаются при помощи потенциометров. Время, необходимое для определения режимов резания и машинного времени, составляет 2 - Змин. [4]
Значение исходной величины при необходимости помещают в скобках после обозначения логарифмической величины. [5]
При краткой форме записи значение исходной величины следует указывать в скабк ах после значения уровня. [6]
Во всех расчетах рекомендуется брать значения исходных величин такими, чтобы ими было удобно оперировать, даже если придется допустить незначительное отклонение от их точных значений, Получаемая при этом ошибка незначительна и на окончательные результаты практически не влияет. [7]
Во всех расчетах рекомендуется брать значения исходных величин такими, чтобы ими было удобно оперировать, даже если придется допустить незначительное отклонение от их точных значений. Получаемая при этом ошибка незначительна и на окончательные результаты практически не влияет. [8]
Функции формальных параметров по передаче в тело процедуры значений исходных величин и получению результата в процедуре без параметров выполняются глобальными идентификаторами. Поэтому перед обращением к процедуре без параметров глобальным идентификаторам, обозначающим исходные величины, должны быть присвоены требуемые значения. При обращении к процедуре без параметров указывается лишь один идентификатор процедуры. Результат выполнения процедуры присваивается в ее теле соответствующим глобальным идентификаторам, которые и используются после обращения к процедуре в последующих действиях. [9]
Условия задач для самостоятельного решения представлены схемами со значениями необходимых исходных величин. Так как каждая схема может характеризовать собой аналогичную работу не одной какой-то конструкции, а нескольких, иногда различных по назначению, то в подавляющем большинстве задач не приводятся словесные условия, ограничивающие использование той или иной схемы для какого-нибудь отдельного случая. [10]
Условия задач для самостоятельного решения представлены схемами со значениями необходимых исходных величин. Так как каждая схема может характеризовать собой аналогичную; работу не одной какой-то конструкции, а нескольких, иногда различных по назначению, то в подавляющем большинстве задач не приводятся словесные условия, ограничивающие использование той или иной схемы для какого-нибудь отдельного, случая. [11]
Но если дистанционные измерения позволяют получать сведения о значениях основных исходных величин, которые характеризуют функционирование устройств, они все же не дают средств для того, чтобы управлять таким функционированием или изменять структуру устройств. [12]
Условия всех задач, предназначенных для самостоятельного решения, представлены схемами со значениями необходимых исходных величин. [13]
Анализ подобных спектров позволяет по форме спектра и положению его характерных точек определить значение исходных величин Яц, Hj и ДЯ. Ряд калибровочных зависимостей, полученных в последних работах, приведен на рис. 11.23. Экспериментально наблюдаемые спектры нитроксильных радикалов в анизотропной среде лучше моделируются лоренцевой формой индивидуальной линии, чем гауссовой [82, 88], и поэтому на рис. 11.23 приведены зависимости только для этого выбора формы линии. [14]
Направление и последовательность перехода от одной шкалы к другой указаны стрелками вдоль линий, соединяющих значения исходных величин на схеме. Точки на номограмме соединяют при помощи прозрачной линейки. [15]
Страницы: 1 2