Многомерная регрессия

Cтраница 1

Многомерная регрессия устанавливает связь между функциями двух и более переменных, являющихся случайными величинами. [1]

Алгоритмы восстановления многомерной регрессии в классе линейных функций ЛИР и ЛИР-3, восстановления регрессии с селекцией выборки ЛИРС и ЛИРС-3 и пошаговой оценки регрессии ПОР и ПОР-3 реализуются программой ВОЛНА. Программа ВОЛНА считывает управляющую информацию с перфокарт, а матрицу наблюдений X - из файла данные и реализует один из алгоритмов восстановления многомерной регрессии без перехода к главным компонентам. [2]

Алгоритмы восстановления многомерной регрессии, использующие разложение векторов выбо рки по главным компонентам, реализуются последовательностью программ СОВА - ВОЛНА. Программа СОВА считывает управляющую информацию с перфокарт, а матрицу наблюдений X - из файла данные. Далее программа СОВА выполняет разложение векторов матрицы X по собственным векторам матрицы ХГХ. Полученная матрица коэффициентов X записывается в файл 10, уничтожая тем самым исходную матрицу наблюдений X. Затем вызывается программа ВОЛНА, которая считывает нз файла 10 матрицу X и реализует заданный с помощью управляющей информации алгоритм восстановления регрессии с использованием главных компонент. [3]

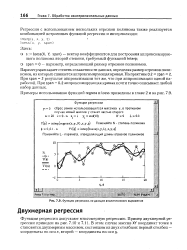
Выполнение алгоритмов восстановления многомерной регрессии, описанных в § 4, без использования главных компонент иллюстрируется следующим примером. [4]

Оценка эффективности уравнения многомерной регрессии может быть произведена по значению остаточной дисперсии. [5]

Функции регрессии, не дающие аналитического выражения. [6]

Функции регрессии допускают многомерную регрессию. [7]

Рассмотрим типичную задачу восстановления многомерной регрессии. Предположим, что изучается объект, который можно описать некоторой совокупностью числовых параметров. Перед исследователем стоит задача: научиться предсказывать значения одних параметров по значениям других и определять возможную ошибку предсказания. [8]

Программа ВОЛНА реализует следующие алгоритмы восстановления многомерной регрессии. [9]

Довольно точные результаты дает применение методов многомерной регрессии, которые позволяют получить компактный и работоспособный алгоритм прогнозирования. [10]

В этой главе описаны алгоритмы восстановления многомерной регрессии в классе линейных и кусочно-линейных функций. Все алгоритмы построены по общей схеме, реализующей метод структурной минимизации среднего риска. [11]

С помощью комплекса ВОЛНА реализуются алгоритмы восстановления многомерной регрессии. Эти алгоритмы разбиваются на две группы. [12]

В отличие от алгоритмов распознавания образов и восстановления многомерной регрессии, алгоритмы восстановления одномерных зависимостей оформлены в виде подпрограмм. [13]

В этой главе дается общее описание программ восстановления многомерной регрессии комплекта ВОЛНА, предназначенное для: пользователя. Описываются форматы входных данных, приводятся примеры составления заданий для ЭВМ и список диагностических сообщений программ. [14]

А - регрессии) допускает естественное обобщение ни случай многомерной регрессии. [15]

Страницы: 1 2 3