Значение - внутренняя сила
Cтраница 1
Значение внутренних сил, приходящихся на единицу площади сечения abed у какой-либо его точки А, называется напряжением в этой точке по сечению abed. Поскольку напряжение представляет собой отношение внутренней силы к некоторой площади, оно измеряется в единицах силы, отнесенных к единице площади. [1]
Получают значения искомых внутренних сил в оболочке; внешняя нагрузка q на ней уравновешивается реактивными усилиями колонн. [3]
При названных условиях значения внутренних сил и моментов в сечениях оболочек могут быть получены решением однородных дифференциальных уравнений. Если оболочки подвергаются неравномерным тепловым воздействиям ( температура в поперечном сечении стенки оболочки распределена неравномерно), в них возникают моменты в кольцевом или меридиональном направлениях. Значения внутренних сил и моментов в сечениях оболочек, подверженных неравномерным тепловым воздействиям, не могут быть получены по безмоментной теории. [4]
Чтобы установить закон распределения и значения внутренних сил, возникающих в поперечном сечении балки, уравнений статики недостаточно. Необходимо использовать условия деформации балки. [5]
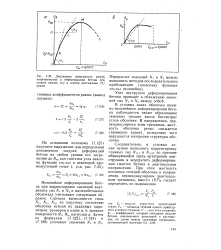 |
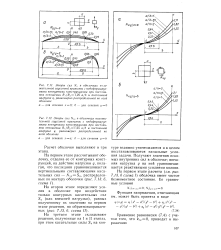
Диаграмма зависимости между напряжениями и деформациями бетона при осевом сжатии ( а и осевом растяжении ( б призм. [6] |
Нелинейное деформирование бетона при корректировке значений внутренних сил Nx и Ny в железобетонных оболочках учитывают следующим образом. [7]
Для расчета пластин с криволинейным контуром целесообразно значения внутренних сил и моментов выразить через производные прогиба по нормали к контуру и вдоль него. [8]
Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще. [9]
Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия будут проще. [10]
Деформации элементов, осадка опор и другие факторы геометрического характера в уравнения равновесия не входят и поэтому не влияют на значения внутренних сил в статически определимых системах. При отсутствии нагрузки внутренние силы в статически определимых системах равны нулю. [11]
Радиус податливой плоскости а, входящий в формулы (3.82) и (3.83), подлежит определению, причем для каждого типа породы значение а будет различно. Он соответствует моменту, когда величина максимального касательного напряжения, развивающегося на поверхности скольжения превышает значение внутренних сил сопротивления среды сдвигу. [12]
Очевидно, что согласно третьему закону Ньютона ( аксиома взаимодействия) внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия будут проще. [13]
Очевидно, что, согласно третьему закону Ньютона ( аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще. [14]
При названных условиях значения внутренних сил и моментов в сечениях оболочек могут быть получены решением однородных дифференциальных уравнений. Если оболочки подвергаются неравномерным тепловым воздействиям ( температура в поперечном сечении стенки оболочки распределена неравномерно), в них возникают моменты в кольцевом или меридиональном направлениях. Значения внутренних сил и моментов в сечениях оболочек, подверженных неравномерным тепловым воздействиям, не могут быть получены по безмоментной теории. [15]
Страницы: 1 2