Значение - сумма - ряд
Cтраница 1
 |
Изображение проекции структуры, полученное на принтере. [1] |
Значения суммы рядов Фурье в узлах решетки могут быть выведены на печать. Для облегчения восприятия результатов точки с равными значениями соединяют замкнутой кривой линией. Полученная картина похожа на топографическую карту, атомы обнаруживаются в вершинах, окруженных несколькими концентрическими линиями. Однако для такого подхода нужен графопостроитель и графические программы, которые требуют затрат машинного времени и памяти для хранения значений электронной плотности. [2]
Re 1 равно пределу, к которому стремятся внутренние значения суммы ряда при приближении к точке Re изнутри по радиусу. На этой теореме основано простое определение сумм некоторых тригонометрических рядов. [3]
Однако в уравнениях для ректификационных колонн величины А обычно неодинаковы, поэтому и значение суммы ряда можно рассчитывать прямым путем. [4]
Так как S-Sn rn, то г представляет собой абсолютную погрешность приближения S &8 значения суммы ряда при помощи его n - й частичной суммы. Следовательно, если величина S представлена в виде суммы сходящегося ряда, то ее можно аппроксимировать частичными суммами с любой наперед заданной точностью. [5]
Что касается первых п членов ряда, то они могут быть любыми ограниченными величинами и их значение на сходимость ряда не отражается, а изменяет лишь на конечную величину значение суммы ряда. [6]
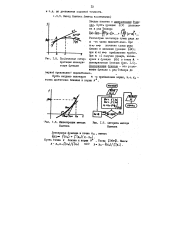
Рассмотрим частичную сумму ряда до К - го члена включительно. При Кв о значение суммы ряда близко к значению функции f ( х); при к оо приближение грубое. [8]
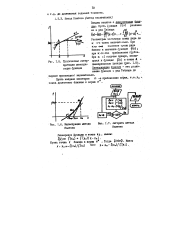 |
Иллюстрация метода Ньютона.| Алгоритм метода Ньютона. [9] |
Рассмотрим частичную сумму ряда до К - го члена включительно. При К % оо значение суммы ряда близко к значению функции f ( х); при к оо приближение грубое. При к 1 получим прямую, касаю - 1.5. Графическая интер - щуюся к функции f ( x) в точке А. [10]
Выяснение сходимости того или иного ряда имеет для использования в теоретических и прикладных вопросах принципиальное значение: только сходящийся ряд мы можем понимать как бесконечную сумму, а именно как предел последовательности его частичных сумм. Более того, в некоторых вопросах значение суммы ряда по сравнению с фактом его сходимости вообще не играет роли. Аналогично в § 10 главы 5 в качестве условия почленной диф-ференцируемости функционального ряда в некоторой точке приводилась равномерная сходимость ряда производных его членов в какой-либо замкнутой окрестности этой точки, но значения суммы ряда производных в остальных точках окрестности были несущественными. [11]
Выяснение сходимости того или иного ряда имеет для использования в теоретических и прикладных вопросах принципиальное значение: только сходящийся ряд мы можем понимать как бесконечную сумму, а именно как предел последовательности его частичных сумм. Более того, в некоторых вопросах значение суммы ряда по сравнению с фактом его сходимости вообще не играет роли. Аналогично в § 10 главы 5 в качестве условия почленной диф-ференцируемости функционального ряда в некоторой точке приводилась равномерная сходимость ряда производных его членов в какой-либо замкнутой окрестности этой точки, но значения суммы ряда производных в остальных точках окрестности были несущественными. [12]
Страницы: 1