Значение - терм
Cтраница 1
Значение терма К & Р равно количеству символов, составляющих соответствующий операнд. [1]
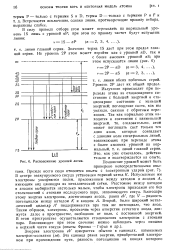 |
Расположение уровней лития. [2] |
Значение терма IS дает при этом предел главной серии. [3]
Значения термов вида 2 и 3 однозначно определяются их начертаниями на стадии написания исходного модуля. [4]
Если значения термов указаны в обратных сантиметрах, то разность двух термов сразу дает волновое число спектральной линии. [5]
Область значений терма а есть область значений а в а. Ясно, что область значений замкнутого константного терма ( не содержащего переменных) представляет собой единственное значение. [6]
Тогда значением терма аЪ будет класс слова ab, равный классу слова aa по построению полугруппы. А равенство Ь6 а не будет истинно, так как значение терма ЬЬ есть класс слова ЬЬ, значение терма а есть класс слова а, а эти классы различны по предположению. [7]
Из формулы для значения термов видно, что уровни энергии здесь не будут равноотстоящими, как в гармоническом осцилляторе. Расстояние между ними медленно уменьшается с увеличением колебательного квантового числа v, что хорошо согласуется с опытными данными. [8]
Диаграмма Мозели и значения термов Х - лучей. [9]
Во всех группах значения термов увеличиваются в соответствии с главными квантовыми числами. [10]
Теперь вводим понятие значения терма при заданных значениях предметных и функциональных символов в заданном основном множестве А. По определению задать значения предметных символов - это значит каждому символу сопоставить определенный элемент множества Л, который и будет называться значением указанного символа. Указать значение тг-арного функционального символа / - это значит сопоставить с ним какую-либо конкретную гс-арную операцию /, определенную на множестве А. Иногда наряду с функциональными символами рассматривают и символы частичных функций. Определение терма при этом остается прежним, но в качестве значения частично функционального символа допускается любая частичная операция соответствующей арности, определенная на множестве А. [11]
Значение выражения вычисляется из значений термов по правилам арифметики целых чисел. Результатом деления считается целая часть частного. Значения выражения п всех его промежуточных результатов не должны выходить за указанные выше пределы. [12]
В целом в результате вычисления значений нумерических термов получается следующее: рассматриваемый вывод переходит в вывод, снова укладывающийся в рамки установленного нами формализма. Концевой фрагмент первоначального вывода переходит в концевой фрагмент преобразованного. Кроме того, все встречающиеся в этом фрагменте нумерические термы являются цифрами, за исключением, быть может, тех термов, которые фигурируют в переходах от аксиом для квантора существования к результатам их полного вычисления. [13]
Если MI есть множество всех значений термов сигнатуры а при значениях переменных из множества А, то ( М а) есть подсистема УЯ и содержится в любой подсистеме, содержащей А. [14]
Так как подалгебры замкнуты относительно значений условных термов и автоморфизмы. [15]
Страницы: 1 2 3 4