Неустойчивый стационарный режим

Cтраница 1

Неустойчивые стационарные режимы не представляют в нашей задаче практического интереса. [1]

Средняя точка пересечения AZf представляет неустойчивый стационарный режим. [2]

Рассмотрена задача управления о стабилизации неустойчивого стационарного режима в реакторе с псевдоожиженным слоем катализатора. Обратная связь в виде функционала от решения обеспечивает устойчивость выбранного режима. Циркуляционная модель слоя, состоящая из системы гиперболических уравнений первого порядка с двумя независимыми переменными, аппроксимируется системой обыкновенных дифференциальных уравнений с помощью метода ортогональных коллокаций. Интегральные ядра функционала обратной связи находятся методом модального управления. [3]

Точка В на рис. 13.8.6 соответствует неустойчивому стационарному режиму, так как отклонение действующего значения С / ос от стационарного значения С / ос в сторону уменьшения ведет к Scr ( Uoc) S p и аэ0, т.е. к дальнейшему уменьшению напряжения Uoc, а отклонение действующего значения С / ос от стационарного значения С / ос в сторону увеличения вызовет дальнейший его рост и переход в следующее стационарное состояние, отмеченное точкой С. Стационарное состояние в точке С является устойчивым, в чем легко убедиться с помощью рассуждений, аналогичных приведенным выше. [4]

Нетрудно видеть, что точке 2 соответствует неустойчивый стационарный режим ХТС. [5]

Наличие обратных связей в сложных схемах делает возможным появление неустойчивых стационарных режимов. Может возникнуть такая ситуация, что найденный оптимальный стационарный режим схемы будет неустойчивым и, следовательно, его нельзя будет реализовать без специальной системы автоматического регулирования. [6]

Мы рассмотрим задачу управления процессом в реакторе с псевдоожиженным слоем катализатора в окрестности неустойчивого стационарного режима, исследуем устойчивость распределенной системы без управления и с введенным с помощью обратной связи управлением. Аппроксимация распределенной модели проводится с помощью метода ортогональных коллокаций. Величина воздействия обратной связи определяется методом модального управления путем сдвига нескольких собственных значений соответствующей задачи в левую полуплоскость, чтобы сделать выбранный стационарный режим устойчивым. Аналогичный подход для управления распределенными системами использован в [5] для реактора с неподвижным слоем катализатора с охлаждающей рубашкой и одинаковой температурой хладоагента по длине реактора, где рассматривалась квазигомогенная модель, состоящая из системы уравнений параболического типа. В [ 61 нами дано управление процессом в реакторе с псевдоожиженным слоем катализатора. [7]

При определении вероятностей ak необходимо учитывать, что некоторые условные решения могут соответствовать неустойчивым стационарным режимам. Вопрос о выделении устойчивых и неустойчивых ветвей среди условных решений будет подробно рассмотрен в пятой главе. [8]

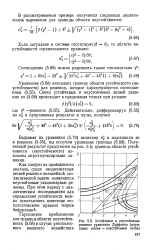Устойчивые и неустойчивые решения уравнения Дуффинга ( штриховые линии - неустойчивые ветви. [9]

Как следует из проведенного анализа, среди неоднозначных ветвей решения нелинейной стохастической задачи появляются неустойчивые стационарные режимы. [10]

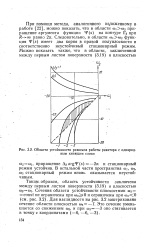Области устойчивости режимов работы реактора с однородным кипящим слоем. [11]

Следовательно, в области coico2 функция W ( s) имеет два корня в правой полуплоскости и соответственно неустойчивый стационарный режим. [12]

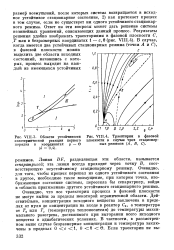Области устойчивости экзотермической реакции первого порядка в координатах ц. - в.| Траектории в фазовой. [13]

Линия DE, разделяющая эти области, называется сепаратрисой; эта линия всегда проходит через точку В, соответствующую неустойчивому стационарному режиму. Очевидно, для того, чтобы процесс перешел из одного устойчивого состояния в другое, необходимо такое возмущение, при котором точка, изображающая состояние системы, пересекла бы сепаратрису, войдя в область притяжения другого устойчивого стационарного режима. Очевидно, что все траектории процесса в фазовой плоскости не могут выйти за пределы некоторой ограниченной области. Действительно, концентрация исходного вещества заключена в пределах от нуля до концентрации на входе в реактор С0, а температура от Т0 или Тс ( температура теплоносителя) до температуры максимального разогрева, достижимого при выгорании всего исходного вещества в адиабатических условиях. [14]

При постоянном внешнем моменте m const, меньшем, чем максимум электромагнитного момента имеются два стационарных значения частоты, причем меньшей отвечает устойчивый, а большей - неустойчивый стационарный режим. Если момент двигателя зависит от частоты uj и монотонно убывает при росте w, то система допускает либо одно устойчивое, либо три стационарных решения, причем большей и меньшей частоте отвечают устойчивые, а средней - неустойчивое стационарное движение. [15]

Страницы: 1 2