Значение - потенциальная функция
Cтраница 1
Значения потенциальных функций, рассчитанных по формуле (4.14), приведены в табл. 4.16. Если потенциальная функция для месторождений с нефтяной оторочкой ( класс А) имеет большее значение, чем для месторождений без нефтяной оторочки ( класс В), то данное месторождение относится к классу А, и наоборот. [1]
 |
Картина распределения потенциала в зазоре под. [2] |
Значения потенциальной функции указываются в узлах сетки, причем в исследуемой, зоне зазора под крайними пакетами сердечника статора нанесено больше узлов, чем в остальной области. На рис. 5 - 2 представлены также линии равного потенциала. [3]
В узлах сетки вычислим значения потенциальной функции нагрузок приемников. [4]
Формулы, связывающие дебиты и значения потенциальной функции на контурах скважин и питания при одновременной работе многих параллельных прямолинейных бесконечных батарей, эксплуатационных и нагнетательных, можно вывести по способу, который кратко здесь опишем. Суть этого способа заключается в том, что в формулах настоящего параграфа совершается предельный переход, причем прямолинейная батарея рассматривается как кольцевая, но с бесконечно большим радиусом. [5]
Для оценки проведенного обучения были вычислены значения потенциальных функций в отдельности для положительных и отрицательных результатов. В таблице против скважин, в которых ГРП положителен, поставлен знак и знак - , если по выбранной методике ожидается отрицательный результат. [6]
Более того, впервые было указано на существование и значение потенциальной функции. [7]
Затем с учетом полученных весов определяются по каждой скважине значения потенциальных функций. [8]
В одном варианте нам известны: постоянный массовый дебит М и значение потенциальной функции ф на одной из граничных поверхностей рассматриваемой области пласта, например, на стенке ( забое) эксплуатационной скважины или галереи. [9]
Если бы проводники цепи были бесконечно тонкими, то определенных нами значений потенциальных функций было бы совершенно достаточно для того, чтобы охарактеризовать электрическое поле линии. [10]
Таким образом, подобно тому как разность потенциалов между любыми двумя точками определяется разностью значений потенциальных функций в этих двух точках, так и полный поток индукции, проходящий сквозь линию, соединяющую две произвольные точки в поле, равен произведению диэлектрической проницаемости е на разность значений функции потока в этих двух точках. [11]
Степень близости исследуемого изделия к данному образу определяется, как уже нам известно, значением потенциальной функции распознавания. [12]
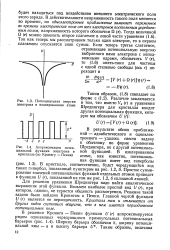 |
Потенциальная энергия электрона в изолированном атоме. [13] |
Простое суммирование значений потенциальных функций отдельных атомов приводит к функции U ( г), показанной на том же рис. 1.2, б сплошной линией. [14]
Однозначность решения дифференциальных уравнений в частных производных, описывающих с помощью функций скалярного или векторного потенциала магнитные поля, определяется граничными условиями. В качестве граничных условий принимаются значения потенциальной функции, а также ее производные на границах расчетной области. На практике встречаются следующие граничные условия: 1-го рода ( условия Дирихле), когда на границах рассматриваемой области имеются только значения функции; 2-го рода ( условия Неймана), когда на границах имеются только производные от функции; 3-го рода ( смешанные граничные условия), когда на одной части границ задана функция, а на другой - производные от функции. Если на всех границах заданы граничные условия только 1-го или 2-го рода, то они называются однородными. [15]
Страницы: 1 2