Значение - автокорреляционная функция
Cтраница 1
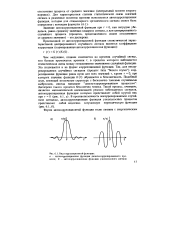 |
Вид корреляционной функции. [1] |
Значение автокорреляционной функции при т - 0, как нетрудно убедиться, равно среднему значению квадрата сигнала, а для центрированного случайного процесса ( процесса, представленного своим отклонением от среднего значения) - его дисперсии. [2]
 |
Коррелограмма временного ряда потребления электроэнергии. [3] |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции, во-вторых, сезонных колебаний периодичностью в четыре квартала. [4]
Это утверждение лежит в основе вычисления значений частной автокорреляционной функции. [5]
Грюнвальд [46] значение а связывает со значением автокорреляционной функции прогнозируемого процесса. Однако при наличии малого числа наблюдений проведение корреляционного анализа временных рядов может оказаться затруднительным. [6]
И наконец, полученные по формуле (3.15) значения автокорреляционной функции ( для различных интервалов времени т sTQ) аппроксимируют аналитически плавной кривой. [7]
Для анализа работы САУ часто важно знать значение автокорреляционной функции / Су ( т), а также спектральной плотности 5к ( о) выходного сигнала. [8]
Очевидно, что в случае отсутствия автокорреляции все значения автокорреляционной функции равны нулю. Разумеется, ее выборочные значения г ( т) окажутся отличными от нуля, но в этом случае отличие не должно быть существенным. На этой идее основан еще один тест, проверяющий гипотезу об отсутствии автокорреляции, - Q-тест Льюинга - Бокса. [9]
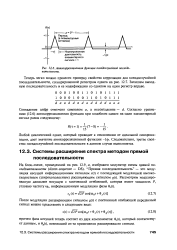 |
Автокорреляционная функция псевдослучайной последовательности. [10] |
Любой циклический сдвиг, который приводит к отклонению от идеальной синхронизации, дает значение автокорреляционной функции - Пр. Следовательно, третье свойство псевдослучайной последовательности в данном случае выполняется. [11]
Аналогичное выражение определяет и дисперсию для взаимно корреляционной функции, только в числителе стоит произведение значений автокорреляционной функции в нуле. Значение корреляционного шума велико. [12]
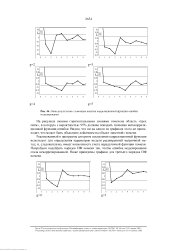 |
Окно результатов с помощью анализа корреляционной функции ошибки моделирования. [13] |
На рисунках синими горизонтальными линиями отмечена область трех сигм, в которую с вероятностью 95 % должны попадать значения автокорреляционной функции ошибки. Видно, что ни на одном из графиков этого не происходит, что может быть объяснено действием на объект цветной помехи. [14]
Вычислить вручную значение Qp-статистики при р, как правило, достаточно трудно ( напомним еще раз, что значение статистики Дарбина-Уотсона дает информацию лишь о значении автокорреляционной функции первого порядка), однако, в большинстве компьютерных пакетов тест Льюинга-Бокса выполняется специальной командой. [15]
Страницы: 1 2