Значение - весовая функция
Cтраница 2
 |
Весовая функция для канала 1 ах - 1 вых противоточного теплообменника. [16] |
Поскольку в выбранных безразмерных единицах времени выполнено условие TI - f - T2 1, то п 1 2ti 2 - Из этого следует, что второе слагаемое дает вклад в значение весовой функции только при временах, превышающих сумму времен протекания через теплообменник жидкости в первом и втором потоке. [17]
 |
Весовая функция для канала 1 вх ( Г1 вых противоточного теплообменника. [18] |
Поскольку в выбранных безразмерных единицах времени выполнено условие TI т 2 1, то TI 1 2ti - ( - tz - Из этого следует, что второе слагаемое дает вклад в значение весовой функции только при временах, превышающих сумму времен протекания через теплообменник жидкости в первом и втором потоке. [19]
Эти условия, очевидно, выполняются, если можно выбрать достаточно большое число N подынтегралов статистической независимости ( Atft Th 1 - ть), таких, что за время от 0 до IN значение весовой функции не упадет до слишком малой величины. [20]
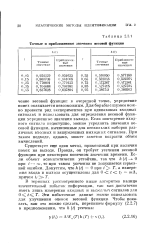 |
Точные и приближенные значения весовой функции. [21] |
Если повторение входного сигнала недоступно, можно усреднить значения весовой функции, вычисленные для нескольких наборов различных входных и зашумленных выходных сигналов. При таком подходе, однако, может заметно возрасти объем вычислений. [22]
Из (10.76), в частности, следует высказанное выше утверждение: что если х ( t) распределен по нормальному закону, то и процесс у ( t) нормален, так как сумма нормально распределенных случайных величин распределена нормально [20] Более того, центральная предельная теорема теории вероятностей ( теорема Ляпунова) утверждает, что распределение суммы большого числа некоррелированных случайных величин приближается к нормальному закону, даже если распределение каждой величины отлично от нормального. Эти условия, очевидно, выполняются, если можно выбрать достаточно большое число N подынтервалов статистической независимости ( Дт ih-u - rft) таких, что за время от 0 до % N значение весовой функции не упадет до слишком малой величины. [23]
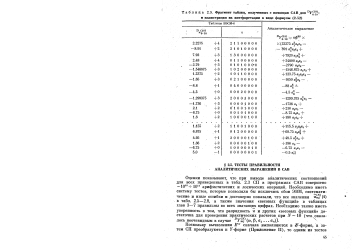 |
Фрагмент таблиц, полученных с помощью CAB для Dlr01 в иллюстрация их интерпретации в виде формулы. [24] |
Оценки показывают, что при выводе аналитических соотношений для всех приведенных в табл. 2.3 СП в программах CAB совершено - 1010 - г - 1011 арифметических и логических операций. Необходимо иметь систему тестов, которые позволяли бы исключить сбои ЭВМ, систематические и иные ошибки и достоверно показали, что все значения x - mj ( t) в табл. 2.5 - 2.8, а также значения весовых функций в таблицах глав 3 - 7 правильны во всех значащих цифрах. [25]
Следовательно, реакция, называемая весовой функцией, не будет учитывать последующий характер изменения коэффициентов, и получить по весовой функции реакцию на какое-либо другое длительное воздействие уже по этому соображению принципиально не возможно. Поэтому изображение весовой функции передаточными свойствами в рассматриваемом случае не обладает. Но, если накопить серию значений весовых функций при различных смещениях, то, выбрав из них по одной точке для момента наблюдения t, можно сформировать параметрическую весовую и параметрическую передаточную функции, применение которых рассмотрено выше. [26]
Использование весовой функции позволяет придать разную значимость различным участкам частотной оси. В частности, это дает возможность задать переходные зоны, поведение АЧХ в которых не имеет значения. В этих зонах значение весовой функции должно быть нулевым. [27]
Представленный на рис. 14.4 алгоритм дискретного преобразования Фурье предусматривает большой объем вычислений. Этот алгоритм содержит большое количество избыточных операций, в том числе и таких, когда одни и те же операции многократно выполняются над одними и теми же значениями величин. Это связано со следующим. N-I) 2, будет содержать большое число периодов N и соответствующие им значения весовой функции Wnk будут повторяться через период N. [28]
Представленный на рис. 14.4 алгоритм дискретного преобразования Фурье предусматривает большой объем вычислений. Этот алгоритм содержит большое количество избыточных операций, в том числе и таких, когда одни и те же операции многократно выполняются над одними и теми же значениями неличин. Это связано со следующим. N - I) 2, будет содержать большое число периодов N и соответствующие им значения весовой функции Wnk будут повторяться через период N. [29]
Страницы: 1 2