Значение - передаточная функция
Cтраница 3
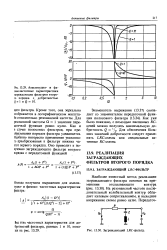 |
Амплитудно - и фа-зово-частотные характеристики заграждающих фильтров второго порядка с добротностью g 1 и Q 10.| Заграждающий LRC-фильтр. [31] |
Кроме того, она зеркально отображается в логарифмическом масштабе относительно резонансной частоты. Для резонансной частоты Q 1 значение передаточной функции равно нулю. Как и в случае полосовых фильтров, при преобразовании порядок фильтра удваивается. Особенно интересно применение указанного преобразования к фильтру нижних частот первого порядка. [32]
Для оценки статических свойств систем регулирования необходимо вычислить статические коэффициенты усиления систем регулирования для всех реально возможных комбинаций точек приложения возмущений и изучаемых величин. Статический коэффициент усиления системы регулирования определяется значением передаточной функции между данными двумя точками системы регулирования при установившемся режиме. Введение в анализ систем понятия статического коэффициента усиления позволяет сделать его более простым и наглядным. [33]
Исходными данными для определения технологических погрешностей собранного подшипника являются спектры осевой и радиальной вибрации, параметры, определяющие условия работы подшипника, и конструктивные размеры. Как следует из полученных результатов, амплитуда вибрации определяется значением передаточной функции W0j и амплитудой возмущающих сил. [34]
Кривые, изображенные на рис. 2 и 3, характеризуют изменение температуры в реакторе при изменении подачи в реактор хладагента и исходных растворов. Кривые I получены расчетным путем по формулам ( 2), ( 4 -, ( 5), - куда были подставлены значения передаточных функций звеньев. [35]
По формуле ( 102) или ( 98) определяются абсолютные чения i - ro настраиваемого параметра при определенных значениях произвольно изменяющихся параметров. Действительно, из теоремы о начальных ( или конечных) значениях следует, что для случая, когда рассматриваются единичные скачкообразные изменения переменных, относительно которых записаны передаточные функции, начальные ( или конечные) значения настраиваемых параметров или ошибки - как функции времени, определяются конечными ( или начальными) значениями соответствующих передаточных функций. [36]
Далее в соответствии с заданным критерием оптимальности системы самолет-летчик рассчитывают или опытным путем подбирают в процессе моделирования требуемую передаточную функцию эквивалентного звена. Параметры модели устанавливаются в соответствии с их найденными оптимальными значениями. По разности значения передаточных функций эквивалентного звена ( оптимальной и фактической) и знании влияния отдельных параметров модели на значение ее передаточной функции выдвигаются технические требования к характеристикам приборно-индикационного оборудования и средств передачи управления. Техническая реализация этих требований позволит приблизить передаточную функцию эквивалентного звена к ее оптимально требуемому значению. [37]
 |
Структурные схемы замкнутых систем авторегулирования. [38] |
Функциональные элементы дозаторов могут реализовываться с использованием различных принципиальных и конструктивных решений, представляемых тем или иным набором элементарных звеньев, в связи с чем структурная схема будет иметь значительное количество вариантов. Так, структурные схемы выпускаемых в настоящее время дозаторов имеют более 40 вариантов. В целях обобщения в дальнейшем, как правило, используется неявное значение передаточной функции и рассматриваются передаточные функции комплексов элементарных звеньев, соответствующие отдельным функциональным элементам. [39]
 |
Контур обратной связи с передаточными функциями К и Ks. [40] |
Величину Е обычно называют эффективной передаточной функцией. Таким образом, обратная связь является положительной. Если же значение передаточной функции К 0, знаменатель ( 1 Л7Г /) 1, ЕК, и обратная связь отрицательная. [41]
Для получения математических моделей сложных трубопроводных систем целесообразно использовать свойства направленных графов. Согласно этому способу вводят граф сигналов, соответствующий системе линейных уравнений и включающий совокупность вершин и ветвей. Вершины представляют собой искомые и задающие переменные. Ветви графа изображают отрезками. Направление ветви указывают стрелкой от источника к стоку. Вершины, с которыми связаны только выходящие ветви, являются источниками, поскольку сигналы таких вершин зависят от сигналов других вершин. Каждой из ветвей придают значение соответствующей частной передаточной функции изучаемой трубопроводной системы. [42]
Страницы: 1 2 3