Значение - собственная частота
Cтраница 1
Значения собственных частот останутся верными при любых значения внешних сил, но смотреть на результат статического расчета будет скучно: в таблицах окажутся одни нули. [1]
Значения собственной частоты для двойных стен столь же важны, как значения критической частоты для однослойных стен. [2]
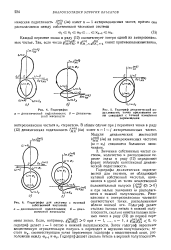 |
Годограф динамической по-дагливости. точка приложения силы совпадает с точкой измерения перемещения. [3] |
Значения собственных частот системы, количество и расположение перемен знака в ряду ( 12) определяют форму годографа комплексной динамической податливости. [4]
Значения остальных собственных частот находятся из оставшихся пяти уравнений. [5]
Значения собственной частоты механических систем, наоборот, могут быть весьма разнообразны ( например, от долей герца до 50 кГц - см. § 4 - 4) и поэтому всегда должны рассчитываться. [6]
Такое значение собственной частоты колебаний используется для определения оптимальной длины дрейфа, при которой достигается значительное группирование с минимальным разбросом скоростей электронов. Последнее особенно существенно для получения эффективного отбора энергии СВЧ при торможении электронных уплотнений полем выходного резонатора. [7]
Соответственно, значение собственной частоты ю / t в выражении ( 49) не обязательно должно быть равно csk, как для звуковой волны, а может определяться соответствующими дисперсионными соотношениями для любой однородной среды. [8]
Ниже указаны значения собственных частот колебаний для некоторых частных случаев. [9]
При некотором значении собственной частоты ядра Fe57 образца будут поглощать у-кванты резонансно, переходя из основного в возбужденное состояние. Резонансная частота ядра Fe57 в теме весьма чувствительна к воздействию соседних атомов и групп. [10]
Таким образом, значение собственной частоты по упрощенной формуле составляет v7 02 рад / с и погрешность не превышает 0 5 %; значения коэффициента затухания практически совпали. [11]
В табл. 4.1 приведены значения собственных частот для предельных случаев закрытой ( Z2 - - оо), открытой ( Z2 - 0) и нагруженной на волновое сопротивление ( Z2 - - Z22) труб. Видно, что из уравнения частот (4.77) получаются, как частные случаи, частоты закрытой и открытой труб. [12]
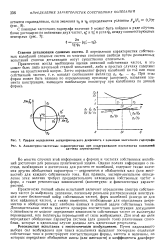 |
График определения логарифмического декремента с помощью частотного годографа.| Амплитудно-частотные характеристики при поддерживании постоянства показаний. [13] |
Практически всегда необходима оценка значений собственных частот, и это может быть либо начальной стадией испытаний, либо в простых случаях содержит ответ на практический вопрос. [14]
Эти значения совпадают со значениями собственных частот генераторов, включенных в жесткую сеть. Однако наибольшая собственная частота системы отлична от остальных частот. [15]
Страницы: 1 2 3 4