Значение - левая часть - уравнение
Cтраница 1
Значения левой части уравнения ( 54), нанесенные на график в зависимости от ионной силы р, должны в первом приближении ложиться на прямую. [1]
Значения левой части уравнения ( 1) зависят от расстояния а и определяются непосредственно из опыта по замерам А и Агаах. [2]
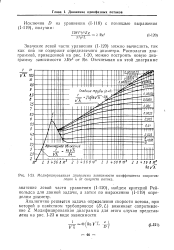 |
Модифицированная диаграмма зависимости коэффициента сопротивления К от скорости потока. [3] |
Значение левой части уравнения ( 1 - 120) можно вычислить, так как оно не содержит определяемого диаметра. [4]
Зная значение левой части уравнения (III.17), по заданному количеству теоретических тарелок по гр афику Кремсера находят значение фактора абсорбции для целевого компонента. По пункту 5 определяют факторы абсорбции всех компонентов, а по ним - значения правой части уравнения ( III. Далее расчет ничем не отличается от изложенного. [5]
Имея значения левой части уравнения (V.6) при разных температурах и разность энергий активации, легко вычислить отношение пред-экспоненциальных факторов. [6]
Обозначим значения левой части уравнения ( б) при х р через у ( х), а при х q - через ф ( х), где у и ф - неизвестные функции. [7]
Нанося на график значения левой части уравнения ( 44) в зависимости от С при условии, что / известно, можно определить величины констант, заключенных в скобки. [8]
Так как при х 8 значение левой части уравнения совпадает со значением правой части, то х 8 - корень данного уравнения. [9]
Определив для различных весов состава значения левой части уравнения, проводят через эти точки прямую штриховую линию, по которой можно определять максимальный вес состава по условию трогания с места. [10]
Кроме того, в программу вводится значение левой части уравнения / ( жн) при х хи либо любое число, совпадающее по знаку со значением функции при х хн. [11]
Используемые подпрограммы и функции: подпрограммы вычисления значений левых частей уравнений располагаются в строках, начиная с 2006, по одной в строке. [12]
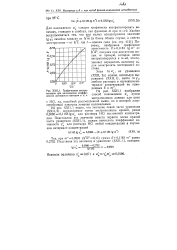 |
Графическая экстраполяция при нахождении коэффициента активности методом э. д. с. [13] |
Из рис. XXII, 1 видно, что значение левой части уравнения ( XXII, 2), определяемое путем экстраполяции кривой, равно 0 2680 0 1183 для раствора НС1 постоянной концентрации. [14]
SO) и выражения (V.40) обоснована экспериментальными данными, полученными для шести систем: значение левой части уравнения ( IV. Этих данных, конечно, все еще мало, но дополнительно можно привести и следующие термодинамические соображения. [15]
Страницы: 1 2 3