Значение - энтропия - вещество
Cтраница 1
Значения энтропии веществ получают из данных по теплоемкостям. [1]
Значения энтропии веществ получают из данных по тепло-емкостям. [2]
Значениями энтропии веществ пользуются для установления изменения энтропии системы в результате соответствующих процессов. [3]
Из данных по температурной зависимости теплоемкости рассчитывают значения энтропии веществ. [4]
Однако в некоторых случаях принимают за нуль значение энтропии вещества при абсолютном нуле температуры. Для этого, впрочем, имеются некоторые теоретические основания ( теорема Нернста), на которых мы останавливаться не будем. [5]
Однако в некоторых случаях принимают за нуль значение энтропии вещества при абсолютном нуле температуры. Для этого, впрочем, имеются некоторые теоретические основания ( теорема Нернста), на которых мы останавливаться не будем. [6]
Следует отметить, что количество данных по значениям энтропии веществ, собранных в сводных таблицах, сравнительно мало. [7]
 |
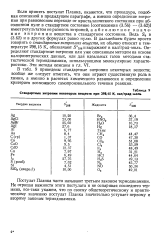
Стандартные энтропии некоторых веществ при 298 15 К, кал / град-моль. [8] |
Если принять постулат Планка, окажется, что процедура, подобная описанной в предыдущем параграфе, а именно определение энтропии при равновесном переходе от кристаллического состояния при абсолютном нуле в стандартное состояние [ соотношения (3.56) - (3.62) ] имеет результатом не разность энтропии, аабсолютное значение энтропии вещества в стандартном состоянии. Ведь S0 в (3.62) и в других формулах равно нулю. В дальнейшем будем просто говорить о стандартных энтропиях веществ, их обычно относят к температуре 298 15 К, обозначают S 298 и выражают в кал / град-моль. Определяют стандартные энтропии или уже описанным методом на основе калориметрических данных, или для идеальных газов методами статистической термодинамики, использующими молекулярные характеристики. Эти методы описаны в гл. [9]
 |
Стандартные энтропии некоторых веществ при 298 15 К, кал / град-моль. [10] |
Если принять постулат Планка, окажется, что процедура, подобная описанной в предыдущем параграфе, а именно определение энтропии при равновесном переходе от кристаллического состояния при абсолютном нуле в стандартное состояние [ соотношения (3.56) - (3.62)) имеет результатом не разность энтропии, аабсолютное значение энтропии вещества в стандартном состоянии. Ведь S0 в (3.62) и в других формулах равно нулю. В дальнейшем будем просто говорить о стандартных энтропиях веществ, их обычно относят к температуре 298 15 К, обозначают 5 298 и выражают в кал / град-моль. Определяют стандартные энтропии или уже описанным методом на основе калориметрических данных, или для идеальных газов методами статистической термодинамики, использующими молекулярные характеристики. Эти методы описаны в гл. [11]
VI, показывает, что Sa лежит между значениями энтропии вещества в точках плавления и кипения и что она составляет приблизительно одну четвертую часть величины энтропии в точке кипения. Это соотношение справедливо даже для водорода. [12]
Нернста заключается в том, что он выдвинул предположение, в дальнейшем подтвержденное практикой и получившее наименование закона Нернста, позволяющее определять абсолютные ( отсчитанные от О К) значения энтропии веществ. Сказанное и является содержанием теплового закона Нернста. [13]
Для определения температуры на основе соотношения (10.1) необходимо измерять изменение энтропии при подведении к соли известного количества тепла. При этом определение энтропии не вызывает затруднений. Для этой цели необходимо знать, каким образом М зависит от Л и Т при начальной температуре. Мы будем предполагать, что это соотношение, являющееся магнитным уравнением состояния, известно. Равенство (9.15) представляет также и разность значений энтропии вещества при начальной и конечной температурах в поле, равном нулю, поскольку размагничивание является изоэнтропическим процессом. [14]
Для определения температуры па основе соотношения (10.1) необходимо измерять изменение энтропии при подведении к соли известного количества тепла. При этом определение энтропии но вызывает затруднении. Для этой цели необходимо знать, каким образом М зависит от II и Т при начальной температуре. Мы будем, предполагать, что это соотношение, являющееся магнитным уравнением состояния, известно. Равенство ( 1.15 представляет также и разность значений энтропии вещества при начальной и конечной температурах в иоле, равном пулю, поскольку размагничивание является изоэнтроппческпм процессом. [15]
Страницы: 1