Зеркальный резонанс

Cтраница 2

К определению зон наблюдения зеркальных резонансов иа остроугольном эшелетте. [16]

Дифракционные зависимости наиболее сложны, когда освещены обе грани канавки, так как могут иметь место зеркальные резонансы любой кратности. [17]

Графики энергий других гармоник имеют заметные максимумы каждый раз, когда для очередной гармоники выполняются условия зеркального резонанса. Всплески кривых становятся все более узкими при возрастании к. [18]

Области применения лазеров в зависимости от требуемой мощности лазерного излучения. [19]

Оптический квантовый генератор ( ОКГ) состоит из рабочего пола ( активная среда), лампы накачки и зеркального резонанса. Сильная световая вспышка лампы превращает электроны активной среды из спокойного в возбужденное состояние. Эти электроны, действуя друг на друга, создают лавинный поток световых фотонов. Отражаясь от резонансных экранов, фотоны пробивают полупрозрачный зеркальный экран и выходят узким монохроматическим когерентным ( строго направленным) световым пучком высокой энергии. [20]

При углах падения, лежащих в / и / / секторах ( освещена только правая грань канавки), имеет место простой зеркальный резонанс в случаях, когда направление распространения одной из гармоник спектра близко к направлению луча, зеркально отраженного от правой грани. Для углов падения, лежащих во / / секторе, наблюдаются двойные и тройные зеркальные резонансы. [21]

Аномальное рассеяние на эшелетте ( а - в и решетке из полуцилиндров ( г ( ф0. [22]

Экспериментально и теоретически обнаружено [206, 257 - 259, 263, 271 - 273], что и для тупоугольных эшелеттов ( наиболее часто используемых в оптике) аномалии Вуда Я-поляризованных волн столь же значительны вблизи условий зеркального резонанса. [23]

Рассеивающие свойства острого эшелетта (. - поляризация, ф 0, а 2х з.. а 90, 2 - 75, 3 - 60. 4 - 45.| Линии равного уровня энергии отраженной от эшелетта волны WQ ( к. а в координатах к, а ( Е - поли-ризация, ф 0, а 2ijJ. [24]

Дело в том, что здесь наблюдается ряд резонансных эффектов: двойной зеркальный, тройной зеркальный и тому подобные резонансы, а для а 90 при целых х - геометрические резонансы I. Кратность зеркального резонанса определяется количеством последовательных отражений от обеих граней луча, прежде чем он уйдет в простанство над эшелеттом. [25]

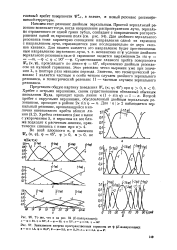То же, что и на 94 (. - поляризация.| Зависимости энергии пространственных гармоник от ф (. - поляризация. [26]

Для двойного зеркального резонанса тоже характерно совпадение направления одной из гармоник с направлением луча, отразившегося уже последовательно от двух склонов канавки. [27]

Энергии пространственных гармоник в случае - поляризации при к 3 4 и ф 0. [28]

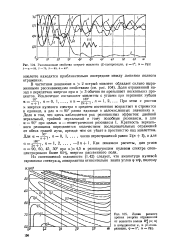
Для минус первой гармоники при х 4 вершина хребта уже практически совпадает с линией зеркального резонанса (3.2), отмеченной на рис. 92 кружочками. Для точного выявления экстремальных точек при зеркальном резонансе во всем диапазоне х необходимы численные расчеты. В общем случае гармоника, для которой выполняется (3.2), в рассеянном поле всегда будет доминирующей. В максимумах резонирующая гармоника может переносить более 90 % энергии рассеянного поля. При коротких длинах волн существование такого резонанса понятно из гео-метрооптических представлений, при длинах волн, соизмеримых с периодом, этот вопрос оставался открытым. Результаты строгого решения показали что зеркальный резонанс является четко выраженным уже при длинах волн, меньших периода. Вообще поверхность WLn образована чередующимися ущельями и хребтами, среди которых хребет с номером п ( вблизи условия (3.2)) является преобладающим, остальные же - незначительные. [29]

Тогда во всем пространстве надэшелеттом существуют четыре попарно встречные плоские волны одинаковой амплитуды: первая падающая, вторая с номером п, распространяющаяся в направлении к источнику, две другие - однородные плоские волны, скользящие вдоль решетки. Наблюдается геометрический резонанс I, являющийся частным случаем двойного зеркального резонанса ( см. гл. Совокупность перечисленных выше факторов в основном определяет характер вторичного поля. [30]

Страницы: 1 2 3 4