Простой резонанс

Cтраница 1

Простые резонансы вблизи со 2coj и со 2со2 на диаграмме не обнаруживаются, а доминируют области неустойчивости, отвечающие комбинационным резонансам на сумме частот. [1]

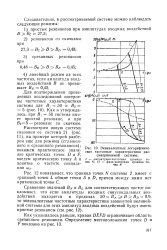Эквивалентные логарифмические частотные характеристики рассматриваемой системы. [2]

Как и утверждалось, при BI 50 система имеет простой резонанс, а при В25 - резонанс со скачком. [3]

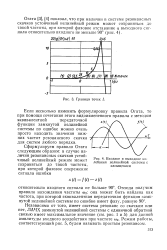Граница точек L.| Входное и выходное колебания нелинейной системы с насыщением. [4]

Режим работы, соответствующий рис. 5, будем называть простым резонансом. [5]

Для определения точных границ возможных режимов работы нелинейных систем ( сглаженный резонанс, простой резонанс, резонанс со скачком, срезанный резонанс и работа в линейном режиме) введены пять критических точек А, С, D, E, F и понятие частоты совпадения шз. [6]

В статье введены понятия следующих видов частотных характеристик нелинейных систем: сглаженный резонанс, простой резонанс и срезанный резонанс. [7]

В - общем случае двойной резонанс в обычной критической точке в случае d измерений имеет форму простого резонанса п случае d - 1 измерений. [8]

В механических системах, для которых уравнение (7.2.32) распадается на независимые уравнения, описывающие изменение каждой обобщенной координаты в отдельности, возможны только простые резонансы. [9]

Движение мультипликаторов р о - -. т при пересечении границы области устойчивости. [10]

В механических системах, для которых уравнение ( 1) распадается на независимые уравнения, описывающие изменение каждой обобщенной координаты в отдельности, возможны только простые резонансы. [11]

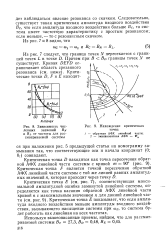Зависимость численных значений Вя и BL от частоты для рассматриваемой системы.| Нахождение критических точек. [12]

Следовательно, существует такая критическая амплитуда входного воздействия Вс, что если амплитуда входного воздействия больше Вс, то система имеет частотную характеристику с простым резонансом; если меньше, - то с резонансным скачком. [13]

На границах областей неустойчивости, отвечающих простым резонансам ( 18), уравнение ( 3) имеет хотя бы одно либо Т -, либо 2Г - периодическое решение. [14]

Это показано на рис. 7.2.9, где случаи а - в отвечают гамилътоловым системам. В области устойчивости все мультипликаторы находятся на единичной окружности. При переходе в область неустойчивости, соответствующую простому резонансу, мультипликаторы становятся кратными. [15]

Страницы: 1 2