Результат - численное моделирование
Cтраница 2
Рассмотрим результаты численного моделирования в рамках следующей постановки задачи. На плоскую мишень нормально к поверхности падает однородный цилиндрический электронный пучок. [16]
Рассмотрим результаты численного моделирования с помощью вышеописанной методики сложной динамики в гидродинамической модели диода Пирса. Бифуркационная диаграмма представляет собой отложенные по оси ординат величины локальных максимумов временной реализации плотности при фиксированном значении параметра Пирса, который откладывается по оси абсцисс. Регулярным режимам на бифуркационной диаграмме соответствуют линии; развилка линии соответствует удвоению периода при переходе через некоторое критическое значение параметра. На бифуркационной диаграмме легко выделяются две области. [17]
Приведем результаты двумерного численного моделирования процесса взаимодействия пучков заряженных частиц с бесстолкновительной плазмой, которое было проведено для проверки выводов трехмерной теории квазилинейной релаксации. [18]
Из результатов численного моделирования также следует, что средняя глобальная температура в следующем столетии будет повышаться со скоростью 0 3 С за 10 лет. В результате к 2005 г. она может возрасти ( по сравнению с доиндустриальным временем) на 2 С, а к 2100 г. - на 4 С. [19]
Из результатов численного моделирования видно, что существуют предпосылки для активного обводнения значительной части пласта IIP. Кроме того, существует реальная опасность обводнения неразбуренных зон с хорошими коллекторскими свойствами и формирование зон макрозащемления газа. [20]
Из результатов численного моделирования процесса разработки известно, что в однородном анизотропном пласте с горизонтальной плоскопараллельной геометрией среды и контактов объем перетоков может изменяться в очень широких пределах в зависимости от положения интервалов перфорации. Совершенно очевидно, что при тех же условиях в расчлененном пласте с линзовидным размещением неколлекторов объем перетоков будет меньше. Объем перетоков еще уменьшится, если все неколлекторы разместить в виде выдержанных слоев. Уменьшение объема перетоков при линзовидном и послойном размещении непроницаемых пород связано с увеличением макроанизотропии среды. Наибольшее увеличение произойдет для среды с послойным размещением непроницаемых слоев, наименьшее - для однородной анизотропной среды. [21]
 |
Машинные траектории полета для электродных систем с наклоном при варьировании начальных и граничных условий. [22] |
По результатам численного моделирования получены в безразмерном представлении номограммы для скорости торможения цепочки капель ( рис. 4.8), толщины погранслоя и профиля скоростей в нем для обширной области, перекрывающей различные классы рабочих жидкостей ( от чернил до расплавов металлов и сжиженных газов), а также короткие и длинные траектории. [23]
В результате численного моделирования на третьем этапе получаются детальные реальные трехмерные картины распределений характеристик сложного нелинейного НДС в конструкциях дефектных участков магистральных трубопроводов при действии всех эксплутационных нагрузок. [24]
В результате численного моделирования были получены распределения концентраций по радиусу керна в различные моменты времени. Анализ кривых показывает, что наличие тупиковых пор, вызванных образованием ганглий, резко осложняет процесс диффузии, выравнивание концентраций идет медленно. [25]
Рассмотрим некоторые результаты численного моделирования процессов деформирования и накопления повреждений неоднородной среды с использованием описанной математической модели. [26]
Полученные в результате численного моделирования в рамках нелинейной нестационарной теории феноменологические выражения для границы клюва синхронизации (7.44) и длины синхронизации (7.43) хорошо подтверждают представленные в начале раздела результаты анализа фазовой синхронизации гиро - ЛВВ в рамках линейной стационарной теории. Более того, в рамках стационарной линейной теории удалось правильно описать пространственную динамику в неавтономной активной среде - было получено, что синхронизация автоколебаний имеет место только на некоторой длине As ( длине синхронизации), которая зависит как от параметров активной среды, так и от характеристик управляющего сигнала. [27]
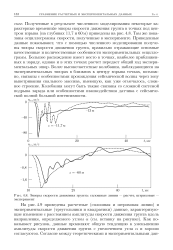 |
Эпюры скорости движения грунта. сплошные линии - расчет, штриховые - эксперимент. [28] |
Полученные в результате численного моделирования некоторые характерные временные эпюры скорости движения грунта в точках под центром взрыва ( на глубинах 11 7 и 60м) приведены на рис. 4.8. Там же показаны осциллограммы скорости, полученные в эксперименте. Приведенные данные показывают, что с помощью численного моделирования получены эпюры скорости движения грунта, правильно отражающие основные качественные и количественные особенности экспериментальных осциллограмм. Большее расхождение имеет место в точках, наиболее приближенных к заряду, однако и в этих точках расчет передает общий ход экспериментальных эпюр. Более высокочастотные колебания, наблюдающиеся на экспериментальных эпюрах в ближних к центру взрыва точках, возможно, связаны с особенностями прохождения сейсмической волны через зону выветривания скального массива, имеющую, как уже отмечалось, сложное строение. Колебания могут быть также связаны со сложной системой подрыва заряда или особенностями взаимодействия датчика с сейсмической волной большой интенсивности. [29]
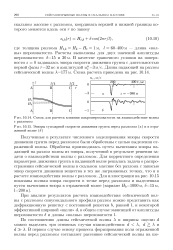 |
Схема для расчета влияния макрошероховатости на взаимодействие волны с разломом.| Эпюры суммарной скорости движения грунта перед разломом ( а и в отраженной волне ( б. [30] |
Страницы: 1 2 3 4 5