Наибольшее значение - модуль
Cтраница 2
Аналогичные примеры влияния интенсивной закарстованности пород на условия формирования подземного стока имеются на территории азиатской части СССР. На территории Верхояно-Чукотской горноскладчатой области наибольшее значение среднемноголетнего модуля 2 0 л / с-км 2, что связано с серией глыбовых поднятий Колымского срединного массива, сложенных закарстовапяыми карбонатными толщами. [16]
Эти ординаты, как будет показано в следующей главе, весьма важны для определения качества процесса. Легко найти и показатель колебательности М: он равен отношению индексов той кривой равного модуля, которая касается оси мнимых и имеет наибольшее значение модуля, к индексу кривой равного модуля, проходящей через начало координат. Частота в точке касания является частотой истинного, или условного, резонанса; при этой частоте амплитудно-частотная характеристика замкнутой системы имеет максимум. [17]
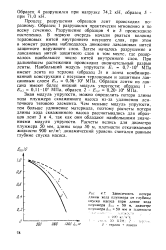 |
Зависимость потери длины хода плунжера от глубины спуска насоса ( при длине хода плунжера 5ПЛ 50 м, диаметре. [18] |
Чем меньше модуль упругости, тем больше удлинение материала, поэтому расчеты потери длины хода скважинного насоса рассчитывались для образцов лент 3 и 4, так как они обладают наибольшими значениями модуля упругости. [19]
По данным Б. П. Беликова [20], наиболее резкое уменьшение модуля упругости наблюдается у карбонатных пород при увеличении пористости начиная с 10 % и выше. Помимо пористости на модуль упругости пород существенное влияние оказывает минералогический состав. Наибольшие значения модуля упругости имеют основные интрузивные породы, несколько меньшие - карбонаты, еще меньшие - кварциты и наименьшие - граниты. [20]
Влияние интенсивной закарстованности пород сказывается в распределении величин подземного стока и в щрноскладчатых областях, что может быть показано на примере Урала и Горного Крыма. Модуль подземного стока для речных бассейнов западного склона Урала, в которых широко распространены интенсивно закарстованные горные породы, превышает в несколько раз таковой для бассейнов, где процессы карсто-образования не проявляются. Наибольшие значения модуля подземного стока ( 10 л / с-км 2 и более) на Урале приурочены к бассейну среднего течения рек Шугоры, Вишеры, Косьвы и других, где развиты карстующиеся породы палеозоя. [21]
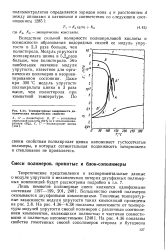 |
Температурные зависимости динамических механических свойств. [22] |
Это наибольшее значение модуля упругости, известное для органических полимеров в неориентированном состоянии. [23]
Между рассмотренными вариантами армирования имеется принципиальное различие в их целевом предназначении. Для создаваемых на их основе композиционных материалов проектируется либо повышение жесткости на растяжение, либо улучшение сдвиговых свойств в определенной плоскости, либо их совместное увеличение во всем объеме. Так, у материалов, армированных в трех ортогональных направлениях согласно варианту 1, следует ожидать наибольшие значения модулей упругости в этих направлениях по сравнению со всеми остальными вариантами пространственного армирования. Такое же утверждение относительно модулей сдвига в трех главных плоскостях упругой симметрии следует для композиционного материала, армированного по варианту 3 с шестью направлениями армирования. [24]
Между рассмотренными вариантами армирования имеется принципиальное различие в их целевом предназначении. Для создаваемых на их основе композиционных материалов проектируется либо повышение жесткости на растяжение, либо улучшение сдвиговых свойств в определенной плоскости, либо их совместное увеличение во всем объеме. Так, у материалов, армированных в трех ортогональных направлениях согласно варианту 1, следует ожидать наибольшие значения модулей упругости в этих направлениях по сравнению со всеми остальными вариантами пространственного армирования. Такое же утверждение относительно модулей сдвига в трех главных плоскостях упругой симметрии следует для композиционного материала, армированного по варианту 3 с шестью направлениями армирования. [25]
Возможность участия естественных запасов в формировании эксплуатационных ресурсов подземных вод определяется не только их общей величиной, но и условиями залегания водоносных горизонтов. Это связано с тем, что при большой глубине залегания кровли водоносного горизонта гравитационные запасы не могут быть использованы, так как при эксплуатации не будет происходить осушения пласта. Поэтому для водоносных горизонтов, кровли которых залегают на глубине более 100 м, в региональных оценках учитывалась только возможная сработка упругих запасов. Наибольшие значения модулей естественных запасов подземных вод характерны для межгорных впадин и предгорных равнин. Несмотря на столь небольшую величину модуля сработки упругих запасов, эксплуатационные ресурсы подземных вод глубокозалегающих напорных горизонтов в артезианских бассейнах платформенного типа формируются главным образом за счет упругих запасов и в связи с огромной площадью распространения водоносных горизонтов обладают значительной величиной. [26]
Величина естественных запасов подземных вод определяется главным образом геолого-гидрогеологическими факторами - литологическим составом водовмещающих пород и типом пустотности, мощностью и площадью распространения водоносного горизонта. При этом под модулем естественных запасов под земных вод понимается количество воды ( в млн. м3), которое можно получить с 1 км2 площади распространения водоносного горизонта при ее осушении. Как следует из этого определения, модуль естественных запасов зависит от водоотдачи водовмещающих пород и их мощности. Наибольшими значениями модуля, естественных ( гравитационных) запасов обычно характеризуются мощные1 толщи гравийно-галечниковых отложений межгорных впадин и предгорных долин. Такие высокие значения модулей гравитационных запасов характерны, например, для четвертичных водоносных горизонтов Чуйской впадины ( мощность гра - вийно-галечниковых отложений 50 - 300 м), Таласской впадины ( мощность около 100 м) и других среднеазиатских, южноказахстанских и закавказских впадин. [27]
Обработка начинается с поиска и прослеживания контуров. Контурные точки составляют незначительную долю в общем числе точек изображения, поэтому здесь возможна существенная экономия времени. Для такой обработки конструируют операторы фильтрации, способные прослеживать контуры на исходном изображении. Простейший из них сводится к поиску точек, для которых модуль градиента функции яркости превышает некоторый заданный порог. Далее осматриваются все точки вокруг найденной и делается шаг в точку с наибольшим значением модуля градиента. Этот процесс повторяется на последующих шагах с тем лишь отличием, что шаг назад запрещен. Так происходит прослеживание контурной линии. [28]
Страницы: 1 2