Аналог - уравнение
Cтраница 1
Аналог уравнения (2.1) приводит к кубическому уравнению, имеющему частное решение qz и два частных решения вида №, где Я удовлетворяет квадратному уравнению. [1]
Аналог уравнения Коши - Римана для ковариантов. [2]
Аналог уравнения Вейля существует и в теории безмассовых фермионов в двумерном пространстве-времени. [3]
Аналогом уравнений (3.12) для рассматриваемого примера является решение задачи сопротивления материалов о напряженно-деформированном состоянии бруса для произвольной точки А. [4]
Аналогом уравнения неразрывности потока в электротехнике является уравнение неразрывности тока, из которого подобно ( 17) следует, как известно, что средние плотности тока в проводнике обратно пропорциональны площадям соответствующих его сечений. [5]
Записав аналог уравнения (5.3.2) для функции V ( t), находим также WWV Q, так что W относится к расщепляющемуся типу и также исключается из леммы. [6]
Получены аналоги уравнений кинетики коагуляции СмолуховСкого с учетом возможности распада образующихся агрегатов и уточнен критерий быстрой коагуляции Дерягина. Найдена связь коэффициентов распада с энергией взаимодействия. [7]
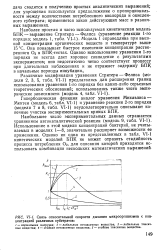 |
Связь относительной скорости дыхания микроорганизмов с концентрацией различных субстратов. [8] |
Гиперболическая функция аналог уравнения Михаэлиса - Ментен ( модель 6, табл. VI-1) и уравнение реакции 2-го порядка ( модели 7 и 8, табл. VI-1) неудовлетворительно описывают конечные участки экспериментальных кривых ВПК. [9]
Оно представляет собой температурный аналог уравнения Кармана - Ховарта для парной корреляции скоростей, обсужденного в разделе 5.4. В работе [10] была проведена прямая экспериментальная проверка уравнения (12.40) измерением всех корреляций, входящих в него. В работе [11] обсуждены возможности получения информации о пульсационных полях температур путем изучения спектральных характеристик этих полей. Следует, наконец, отметить, что, как показывают опытные данные о нахождении функции w ( r, t), в грубом приближении ее можно считать равной детально рассмотренной в главе 5 функции / ( r, t), которая характеризует пульсационное поле скоростей. [10]
Уравнение (32.5) есть аналог уравнения (22.10) плоского случая. [11]
Равенства (4.81) составляют аналог уравнений равновесия (4.3) в полярных координатах. [12]
 |
S. Температурная зависимость удельных избытков термодинамических параметров в поверхностном слое. свободной энергии а, полной энергии Е, энтропии Ч я скрытой теплоты образования поверхности щТ. [13] |
Выражение (1.4) - аналог уравнения Гиббса-Гельмгольца. [14]
Равенства (4.81) составляют аналог уравнений равновесия (4.3) в полярных координатах. [15]
Страницы: 1 2 3 4