Максимальное значение - заряд
Cтраница 1
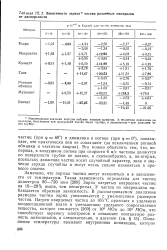 |
Зависимость заряда частиц различных минералов от дисперсности. [1] |
Максимальные значения зарядов набраны жирным шрифтом. В числителе приведены результаты, полученные при продувании частиц через трубку, в знаменателе - при ссыпании через трубку. [2]
Следовательно, для надежного определения максимального значения заряда, переносимого искровым разрядом в данных условиях, эксперименты необходимо проводить с жидкостью, поверхность которой неподвижна, а потенциал ее стабилизирован. [3]
Мы видим, что отношение двух последовательных максимальных значений заряда не зависит от номера максимумов, или, иными словами, эти максимальные значения уменьшаются в геометрической прогрессии. [4]
Мы видим, что отношение двух последовательных максимальных значений заряда не зависит от номера максимумов, или, иными сло-вами, эти максимальные значения уменьшаются в геометрической, прогрессии. [5]
Мы видим, что отношение двух последовательных максимальных значений заряда не зависит от номера максимумов. [6]
Интегрируя в пределах от-у до - J - - , определим максимальные значения зарядов, которые идут на зарядку емкостей в течение одного периода. [7]
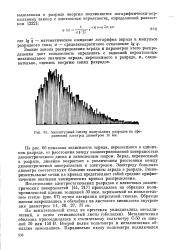 |
Амплитудный спектр импульсных разрядов на сферический электрод диаметром 10 мм. [8] |
Знание закона распределения заряда и параметров этого распределения дает возможность определить с заданной вероятностью максимальное значение заряда, переносимого в разряде, и, следовательно, оценить энергию таких разрядов. [9]
Структура продуктов медленного протонирования анион-радикалов в формально апротонных условиях может соответствовать присоединению протонов по положениям, отличным от положений, для которых расчет методом МОХ дает максимальное значение заряда. [10]
Формулы ( VI 2) и ( VI 3) позволяют оценить максимальный заряд частиц или капель, по которому можно судить о значении кулонов-ской силы [ см. уравнение ( VI. Однако практически трудно достигнуть максимального значения заряда. Это объясняется тем, что в сильном электрическом поле заряженные частицы могут самопроизвольно разряжаться. Кроме того, напряженность поля, входящая в формулу ( VI 2), будет отличаться от напряженности электрического поля Е0, не содержащего частицы. Дело в том, что частицы искажают электрическое поле, и его напряженность будет неравномерна. В результате искажения электрического поля ионы осаждаются неравномерно и преимущественно на стороне частиц, противоположной силовым линиям поля. [11]
 |
Воздействие на линейную емкость напряжений накачки и сигнала ( а и схема замещения для слабого сигнала ( б. [12] |
Реализация скачкообразного изменения С ( f) связана с техническими трудностями и в практике не применяется. Значительно проще модулировать емкость по гармоническому закону. Необходимо лишь соблюдать основной принцип: уменьшать емкость в области максимальных значений заряда ( напряжения) конденсатора и увеличивать в области минимальных значений. [13]
 |
Стилизованная форма вольт-куло-новой характеристики коронирующей линии. [14] |
Так как, удаляясь от оси провода, заряд теряет свой потенциал, то при наличии короны общий заряд при данном напряжении U должен быть больше, чем в случае, когда весь заряд сосредоточен на проводе. Поэтому после момента зажигания короны кривая суммарного заряда пойдет выше синусоиды приложенного напряжения, как это показано пунктиром на рис. 8 - 5 а. После погасания короны заряд в объеме остается практически неизменным, в момент U он начинает уменьшаться, а в момент / е меняет знак на противоположный. Изменение заряда во времени при наличии короны делается несинусоидальным, максимальное значение заряда увеличивается и кривые заряда и напряжения не совпадают по фазе. Благодаря этому в линии появляются высшие гармоники тока, увеличивается эффективная емкость линии и возникают потери энергии. [15]
Страницы: 1