Максимальное значение - модуль
Cтраница 1
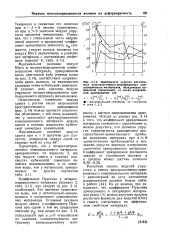 |
Зависимость упругих постоянных пространственно-армированных композиционных материалов, обладающих кубической симметрией, от числа направлений армирования ( п. [1] |
Максимальное значение модуля Юнга в четырех направленном композиционном материале, армированном вдоль диагоналей куба ( темные точки на рис. 3.14), соответствует направлениям вдоль волокон, не являющимся главными осями кубической симметрии. В главных осях значение модуля упругости четырех направленного композиционного материала весьма низкое. [2]
Максимальное значение модуля Юнга ( 1060 ГПа) может быть получено лишь в случае бездефектной структуры кристалла и ориентации атомных плоскостей строго вдоль оси волокон. [4]
Выбираем максимальное значение модуля Dmax и по критерию Колмогорова [65] определяем согласие теоретического и эмпирического законов распределения. [5]
Определить максимальное значение модуля напряженности Ет и координаты хт точек, в которых оно наблюдается. [6]
Определить максимальное значение модуля напряженности Ет и координаты хп точек, в которых оно наблюдается. [7]
Обозначив максимальное значение модуля комплексного коэффициента передачи фильтра через Ко К. [8]
Далее определяем максимальное значение модуля прогиба балки у тах и соответствующую координату сечения хтах. [9]
Если фактически наблюдаемое максимальное значение модуля разности теоретического и эмпирического распределений при заданном п и выбранном уровне значимости а равно или больше критического, то гипотезу о соответствии эмпирического распределения теоретическому отвергают. В противном случае экспериментальные данные считают не противоречащими выдвинутой гипотезе. [10]
Ясно, что максимальное значение модуля функции / равно А. Константу А называют амплитудой колебания. [11]
Ясно, что максимальное значение модуля функции f, задаваемой формулой ( 3), равно А. Константу А называют амплитудой колебания, константу со - циклической частотой колебания, а константу ф - начальной фазой колебания. [12]
Показателем колебательности называется максимальное значение модуля амплитудно-частотной характеристики замкнутой системы. В ряде случаев амплитудно-частотная характеристика системы имеет пик при некоторой частоте сор. Показатель колебательности представляет собой, таким образом, наибольшее отношение амплитуды выходного колебания к амплитуде входного. В эти режимах М служит прямым качественным критерием, имеющим ясный и глубокий физический смысл. [13]
По стандарту принято выбирать максимальное значение модуля конических зубчатых колес. [14]
Далее, исходя из оценок максимального значения неравновесного модуля на основе расчета дискретных моделей, следует признать, что природа упругости в коротковременной части переходной зоны не является чисто энтропийной и в значительной степени имеет черты упругости полимерных стекол. Поэтому распространение теории на эту область требует принципиального изменения молекулярных моделей. [15]
Страницы: 1 2 3 4