Расчетное значение - модуль
Cтраница 1
Расчетное значение модуля увеличивают на 30 % из-за повышенного изнашивания зубьев. [1]
Расчетные значения модуля и межосевого расстояния необходимо привести к величинам, предусмотренным соответствующими стандартами. В случае корректировки некоторых исходных величин ( z, m, , А) необходимо произвести повторно прочностной расчет, как проверочный. По окончательным данным геометрических расчетов выполняют чертежи колес ( см. стр. [2]
Расчетные значения модуля упругости Е и температурного коэффициента линейного расширения а при повышенных температурах принимают по данным гл. [3]
Расчетные значения модулей упругости и сдвига этих материалов представлены в табл. 9.18. Расчет проводили без учета пористости матрицы. При расчете принято, что упругие характеристики углеродных волокон не изменяются с повышением температуры. Совпадение расчетных и экспериментальных значений модулей упругости и сдвига для углепластика на основе полимерной матрицы, как видно из данных табл. 9.18, хорошее. [4]
Ктах представляет собой расчетное значение модуля упругости в конце процесса от-вердцения при данной температуре. [5]
По этой же причине имеет место некоторое превышение расчетных значений модулей упругости материалов, изготовленных на основе кремнеземных, кварцевых и углеродных волокон. При близких значениях коэффициентов армирования в трех направлениях лучшее описание модулей упругости дает второй подход, использование которого в случае больших различий в коэффициентах армирования порождает существенную погрешность для модуля упругости в направлении наименьшего содержания арматуры. Для материалов с малым ц в одном направлении армирования хорошее совпадение расчетных и экспериментальных значений EI наблюдается при использовании зависимостей (9.24), (9.25) первого подхода. Эти зависимости описывают верхний и средний уровни изменения коэффициентов Пуассона. При 1 % jxs ( АЗ совпадение расчетных к экспериментальных значений Vfj удовлетворительное. [6]
Существуют также другие эффекты, способные вызывать отклонения расчетных значений модулей упругости наполненных композиций от экспериментальных. [8]
Кроме того для пар, располагаемых ближе к двигателю, расчетное значение модуля часто получается много меньше, чем реально допустимое из условий технологии нарезания зубьев точных передач. Это условие особенно характерно для маломощных приводов. [9]
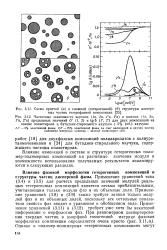 |
Схема простой ( а и сложной ( гетерогенной ( б структуры дисперсных частиц гетерофазной композиции.| Частотные зависимости верхних ( 1в, 2в, 1 ъ, 2 в и нижних ( 1н, 2н. [10] |
Влияние изменений в составе и структуре гетерогенных полимер-полимерных композиций на расчетные значения модуля и возможности использования получаемых результатов анализируются в следующих разделах. [11]
В целях установления степени реализации упругих свойств углеродных волокон в табл. 6.16 представлены также расчетные значения модулей упругости и сдвига. [12]
Таким образом, при расчетах, связанных с учетом сжимаемости жидкости, следует как можно внимательнее выбирать расчетное значение модуля упругости. [13]
При использовании уравнений (3.12) и (3.14) для расчета вязкоупругих свойств композиций с высоким содержанием наполнителя получаются значительные ошибки. Расчетные значения модуля в зависимости от концентрации наполнителя оказываются всегда меньше экспериментальных. Поэтому обычно в уравнение вводится эмпирический поправочный коэффициент, учитывающий объемную долю, эффективно занимаемую наполнителем. По уравнениям (3.12) и (3.14) эта доля легко рассчитывается. [14]
Для углепластика с углеродной матрицей расчетные значения упругих характеристик плохо согласуются с опытными данными. Расчетное значение модуля упругости оказывается существенно ниже экспериментального. Для модуля сдвига получается противоположный результат - экспериментальные значения более чем в 2 раза ниже расчетных. Такое явление объясняется тем, что в процессе создания углеродной матрицы происходит науглероживание волокон, что способствует повышению их жесткости. Кроме того, жесткость углеродной матрицы оказывается значительно выше жесткости исходной полимерной матрицы. [15]
Страницы: 1 2