Произвольное значение

Cтраница 1

Произвольное значение t: выбираем таким образом, чтобы она соответствовало прямой части графика. Определяем соответствующее tl забойное давление раас. [1]

Произвольное значение а для х в R, выбранное между AJ и А 2, будет удовлетворять требованиям нашей леммы. Gv ( A ( x)) и всех функций fj ( x, u ( x)), fj ( x, v ( x) -), вариация знаков которых удовлетворяет теореме Штурма. Мы найдем бесконечно много значений а переменной х в R, которые сохраняют знаки этих рациональных функций. [2]

Выбранное произвольное значение для одной из них сейчас же определяет значение другой величины. [3]

Произвольному значению с соответствует значение Ы1, при котором вихревая дорожка устойчива. [4]

Задавая произвольное значение, например Р3, откладываем его на оси р ( рис. 3, б) и находим а3 на оси ординат. [5]

Пусть произвольное значение j / o ( с, d ] фиксировано. [6]

Дав произвольные значения всем переменным, переменить затем значения фиктивных переменных, сохранив остальные значения. [7]

Выбирая произвольные значения Нг1г, находим соответствующие им значения Я2 / 2 и HS13 из уравнений 1 и 2 и строим оси координат с тройной осью абсцисс, сдвигая начала отсчетов на абсциссах для Я2 / 2 и На. [8]

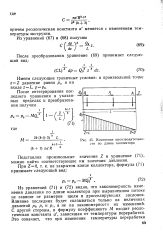Изменение производительности по длине коллектора. [9]

Подставляя произвольные значения Z в уравнение ( 71), можно найти соответствующие им значения давления. [10]

Выберем произвольное значение входной величины ха а и отложим его на первом графике. Ордината графика в этой точке F ( a) b является аргументом для второго графика. С этим значением аргумента Ь входим во второй график и ищем следующую функцию: F2 ( b) c, которая будет являться аргументом для третьего графика, по которому окончательно находим Рз ( с) ха и переносим ее в четвертый квадрант. Повторяя аналогичные построения, в четвертом квадранте построим общую статическую характеристику в координатах ху, хп. [11]

Способ произвольных значений для нахождения А - л, В, С1 / г отличается от предыдущего тем, что каждое требуемое уравнение получаем, давая произвольное значение для х в правом и левом числителях. [12]

Для произвольного значения k точное решение уравнения (4.59) затруднительно. Однако легко может быть построено приближенное решение. [13]

Для произвольного значения / доказательство индуктивного перехода аналогично. Оно использует аргументы, доказанные на предыдущих шагах. [14]

Для произвольных значений k 1 выражения для дальних асимптотик для остальных коэффициентов отсутствуют. [15]

Страницы: 1 2 3 4