Абсолютное значение - ошибка
Cтраница 2
 |
Схема переключателя полярности эталонного напряжения. [16] |
В соответствии с этим эталонное напряжение, подводимое к преобразователю, будет также изменяться на величину падения напряжения на переключателе. Следовательно, абсолютное значение ошибки преобразования из-за неточности переключателя полярности эталонного напряжения будет равно падению напряжения на нем при максимальном токе, потребляемом преобразователем. Снижение в два раза абсолютной величины падения напряжения на ключах можно получить, изменив способ включения триодов в переключателе и способ установки переменных сопротивлений в базовых цепях триодов. [17]
При сошт - ошибка наибольшая и достигает - 3 дб; при ш 2шт - ошибка уменьшается до 1 дб. Таким образом, абсолютные значения ошибки незначительны. [18]
Основная ошибка интегрирования вызывается напряжением UTp, обусловленным наличием нагрузки на валу двигателя. Как показывает выражение ( IV-24), абсолютное значение ошибки от UTp возрастает во времени. [19]
В настоящее время в лаборатории систем управления и информации университета Пэрдью исследуется ряд самообучающихся систем управления. Результаты показывают, что система самообучения, в смысле интегрального абсолютного значения ошибки, характеризуется лучшим качеством, чем соответствующая адаптивная или регулирующая система. Изменение сигнала, в отличие от изменения параметров системы, обладает некоторыми преимуществами в смысле времени самообучения и интегрального значения абсолютной ошибки. Следует учитывать, что одним из наиболее важных вопросов является эффективное использование ограниченной памяти счетно-решающих устройств. В настоящее время исследуется возможность применения принципа опознавания образов к процессу самообучения в системах управления. Точно таким же образом была разработана схема разделения всего диапазона работы системы управления на отдельные области. При этом управляемый объект может быть нелинейным или изменяющимся во времени. Вонхэм и Фу [38] предложили, чтобы адаптивная система с предсказанием воздействия окружающей среды самообучалась, если характер предсказания будет улучшаться с течением времени; при этом данные предсказания могут использоваться для более эффективной адаптации. [20]
На практике наиболее широкое распространение при оценке качества работы ристем регулирования получили интегральная и интегральная квадратичная ошибки. Принципиальное отличие между ними состоит в том, что вторая учитывает абсолютное значение ошибки. Например, две кривые переходного процесса с различными амплитудами колебаний параметра могут иметь одинаковые интегральные ошибки, но разные интегральные квадратичные ошибки. [21]
Таким образом, при пренебрежении содержанием саки в прб-дуктах сгорания значение а получается больше истинного, при пренебрежении содержанием окиси углерода - меньше истинного. При одинаковой доле углерода, продуктами неполного сгорания которой пренебрегают, абсолютное значение ошибки больше при допущении неполноты сгорания только в форме сажи, чем при допущении неполноты сгорания только в СО. [22]
В то же время экспериментальная проверка показывает, что общий ход зависимости ошибки измерения от абсолютного значения оптической плотности очень близок к теоретическому. Он практически не зависит от класса прибора и лишь отличается по абсолютному значению ошибки АЛ: чем выше класс прибора и точнее отсчет по шкале, тем меньше абсолютное значение относительной ошибки при сохранении примерно постоянным общего хода зависимости. [23]
В то же время экспериментальная проверка показывает, что общий ход зависимости ошибки измерения от абсолютного значения оптической плотности очень близок к теоретическому. Он практически не зависит от класса прибора и лишь отличается по абсолютному значению ошибки АЛ: чем выше класс прибора и точнее отсчет по шкале, тем меньше абсолютное значение относительной ошибки при сохранении примерно постоянным общего хода зависимости. [24]
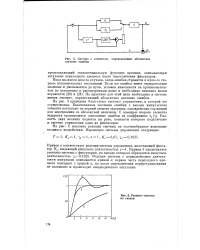 |
Реакция системы на скачок. [25] |
Пока мы имеем дело со случаем, когда ошибка стремится к нулю со стороны положительных отклонений. На практике для этой цели необходимо в систему ввести элемент, определяющий абсолютное значение ошибки. [26]
И аналогично абсолютное значение разности ( 11) при малых / г должно хорошо представлять сумму абсолютных значений локальных погрешностей соответствующих методов. Сопоставляя значения величин ( 11) и ( 12), вычисленных при соблюдении условий малости абсолютных значений ошибок начального условия и округлений, с соответствующими величинами главных членов погрешностей и требуемой точностью результата, можно, в частности, высказать суждение об удаче выбора шага h с большей достоверностью, чем в случае двусторонних приближений ( 9), когда мы не имели непосредственно по ходу вычислений информации типа ( 11) о локальной погрешности метода. При этом, конечно, приходится считаться с тем, что даже грубое вычисление главных членов погрешностей является очень трудоемкой задачей. Поэтому при выборе шага часто руководствуются и другими соображениями. [27]
Напомним, что при вычислении дисперсии, возводя в квадрат ошиб-и, мы тем самым делаем величины неотрицательными. Существует, однако, другой способ сделать их неотрицательными независимо от того, были ли ошибки первоначально отрицательными или положительными. Действительно, возьмем абсолютное значение ошибки ( модуль) и рассмотрим следующую весьма простую процедуру оценивания стандартного отклонения. [28]
Точность результатов титрования определяется точностью определения эквивалентной точки титрования. В аналитической практике конечная точка титрования должна быть возможно ближе к теоретической эквивалентной точке. Разность между конечной точкой и эквивалентной точкой определяет абсолютное значение ошибки титрования. Эту разность можно, например, выразить в объеме раствора титранта, т.е. в виде разности объема титранта j p добавленного до момента достижения конечной точки, и объема Fjp, который необходимо добавить для достижения эквивалентной точки. Если эта разность пот ложительна, то V Vj - конечная точка лежит за эквивалентной точкой и ошибка титрования положительна. При V, Vj ошибка титрования отрицательна. [29]
Эти нормальные ошибки наблюдения тем меньше, чем более усовершенствованы используемые методы, то есть чем больше абсолютная точность наблюдений. Поэтому мы можем взять достаточно грубый пример, скажем, измерение длины в несколько метров посредством деревянного метра с миллиметровыми делениями. Известно, что если против миллиметрового деления приходится достаточно тонкая черточка, то можно отметить и десятую миллиметра, но при нескольких промерах возможна общая ошибка в несколько десятых. Закон ошибок тождествен с законом Лапласа - Гаусса для отклонений при повторных испытаниях. Если мы определим десятичную единицу ошибки и условием, что вероятность абсолютному значению ошибки превзойти и равна одной десятой, то мы заключим, что вероятность превышения этой абсолютной величиной числа 2и равна одной тысячной, вероятность превышения 3 - одной миллионной. При этом положительные и отрицательные ошибки одинаково вероятны. [30]
Страницы: 1 2 3