Произвольно заданное значение

Cтраница 1

Произвольно заданные значения, непрерывные на некоторой замкнутой поверхности Т T n i, образующей границу ограниченной области Д всегда можно рассматривать как значения на поверхности Т некоторой функции, гармонической в области D. Плюригармонические функции составляют, очевидно, подкласс гармонических функций; поэтому, вообще говоря, не существует плюригармонической функции в замкнутой области D, принимающей на поверхности Т наперед заданные значения. [1]

Левая и правая части этого уравнения рассчитываются независимо для произвольно заданных значений а, близких к ориентировочному значению ( VI. По пересечению двух рассчитанных кривых определяется искомое значение а. Поскольку при этом получаются два значения коэффициента, из них выбирается ближнее по величине к ориентировочному. [2]

Левая и правая части этого уравнения рассчитываются независимо для произвольно заданных значений а, близких к ориентировочному значению (5.26), и величины их наносятся на график. [3]

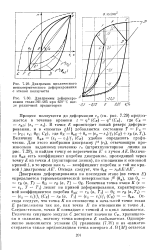Диаграмма циклического неизотермического деформирования с этапом ползучести.| Диаграммы деформиро-вания стали ЭП-485 при 650 С после различной предыстории. [4]

Для этого изобразим диаграмму / А ( г0), отвечающую произвольно заданному значению г о ( штрихпунктирная линия на рис. 7.29), и найдем точку ее пересечения Е с лучом АЕ. [5]

По ней можно легко определить момент, начиная с которого ошибка становится меньше произвольно заданного значения. [6]

Рассматривая равновесие одного из нижних узлов фермы ( рис. 67, в), убеждаемся, что при произвольно заданных значениях Л - 2, / V3, N4, N7, например при jV20, М3ф0, Ni. [7]

Но предыдущее рассуждение вовсе не показывает, что должна суще-твовать тригонометрическая сумма б п ( б), принимающая произвольно заданные значения Sn ( 0), Sn ( a. [8]

Но ведь всегда можно найти кривую у у ( х), у которой у ср, У р и у р имеют произвольно заданные значения в определенной точке. Отсюда вытекает, что выражение Fyy, служащее коэффициентом при у, должно равняться нулю тождественно. [9]

Рассмотренная в предыдущих разделах модель распределения ограниченных ресурсов предполагала заданным множество Sf, определяющее бюджетные ограничения для всех подсистем. При этом в случае произвольно заданных значений 5 - получаемое равновесное распределение не являлось решением общей задачи W, так как не гарантировано достижение максимума ГЦФ. [10]

Задача обычно решается итерационным методом отдельно для каждого часа при произвольно заданном значении A2 j, неизменном в течение суток. Если, например, имел место перерасход воды, то уменьшается нагрузка данной ГЭС, а следовательно, увеличивается коэффициент KZ J и наоборот. После изменения последнего производится полный перерасчет нагрузок всех электростанций для каждого часа суток. Так, последовательным приближением и решается задача оптимального распределения нагрузок электростанций, одновременно определяется истинное значение коэффициентов Л2 3 - для всех ГЭС системы. [11]

Заметив это, вспомним, что когда 2 не зависит от t, траектории связки составляют многообразие со2 - 2 измерений, и потому в пространстве Ги конфигураций одна и только одна из них проходит через заданную точку в заданном направлении. Если каждой точке Р0 сопоставим на соответствующей траектории ту точку Р, в которой действие достигает некоторого произвольно заданного значения а, то геометрическим местом таких точек Р будет новая гиперповерхность. Существует замечательное свойство, что рассматриваемые траектории будут все ортогональными также и к этой гиперповерхности. [12]

Остается теперь показать, как применять эти результаты к решению краевых задач, в которых имеются круговые цилиндрические поверхности. Для иллюстрации ограничимся случаями, когда жидкость целиком находится в бесконечно длинном цилиндре, на поверхности которого поле скорости принимает произвольно заданные значения. Распространение метода на другие ситуации включает просто использование решений уравнений Лапласа, соответствующих рассматриваемой области, например неограниченной области вне цилиндра или области, заключенной между двумя концентрическими цилиндрами. Отметим, что для двумерного обтекания кругового цилиндра неограниченной средой решения не существует. [13]

Точно так же является неопределенным расстояние от циклических точек и до всякой ( другой) конечной точки; то же самое имеет место для расстояния от любой точки мнимой окружности сфер ( принадлежащей бесконечно удаленной плоскости) до любой конечной точки пространства. Этому нисколько не приходится удивляться, ибо мы ведь одновременно требовали от циклических точек, чтобы они находились на расстоянии г от некоторой конечной точки ( лежали на круге радиуса г с центром в этой точке, где г может принимать произвольно заданное значение) и были также бесконечно удалены от этой последней; это кажущееся противоречие наша аналитическая формула может уничтожить лишь тем, что она приводит к полученной выше неопределенности. Эти простые вещи следует себе раз навсегда вполне уяснить, тем более, что о них часто говорят и пишут много неправильного. [14]

Статистический характер не противоречит также и возможности появления макроскопических флуктуационных состояний с меньшей энтропией. Феноменологические уравнения необратимых процессов не учитывают возможность появления флуктуации в системе. Они совместимы с принципом микроскопической обратимости только в том случае, если принять, что средняя эволюция локально-равновесных флуктуации отвечает следующей картине: в момент времени т TO возникает неравновесное флуктуацион-ное состояние с произвольно заданными значениями параметров а, затем оно начинает релаксировать к равновесию в соответствии с феноменологическими законами; эволюция флуктуации до этого момента ( т т0) определяется обращенным во времени ходом релаксации, которая имеет место после то - Естественно, что это представление может быть справедливо только для крупномасштабных флуктуации ( разд. Кроме того, оно предполагает быстрый спад вероятности флуктуации с увеличением отклонения от равцо-весия. [15]

Страницы: 1 2