Наиболее вероятное значение - случайная величина
Cтраница 1
Наиболее вероятное значение случайной величины называется модой. [1]
Наиболее вероятное значение случайной величины совокупности называется модой. Ей соответствует максимальное значение плотности. [2]
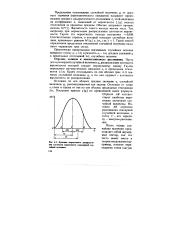 |
Функция нормального распределения плотности вероятности одномерной случайной величины. [3] |
Отрезок АВ соответствует наиболее вероятным значениям случайной величины. [4]
Модой теоретического распределения называется наиболее вероятное значение случайной величины, обозначаемое символом № оХ; модой тйХ эмпирического распределения называется значение, имеющее наибольшую частость. [5]
Это означает, что наиболее вероятным значением случайной величины, распределенной по нормальному закону, является значение, равное математическому ожиданию. [6]
Модой ( Мо) называется наиболее вероятное значение случайной величины или то значение этой величины, частота которого наибольшая. [7]
Математическое ожидание часто интерпретируется как среднее или наиболее вероятное значение случайной величины. [8]
Таким образом, среднее значение в нормальном распределении является наиболее вероятным значением случайной величины. [9]
На выходе ВУ мы должны получить корреляционное уравнение, дающее возможность вычислять наиболее вероятные значения выходной случайной величины в зависимости от других случайных величин. [10]
Точка на оси х, соответствующая максимуму кривой плотности распределения, называется модой, то есть мода - это наиболее вероятное значение случайной величины. Однако, мода существует не у всех распределений. [11]
Для непрерывной случайной величины модой называют точку максимума плотности распределения ее вероятностей. Распределения с одной модой называются одномодальными; они играют наиболее важную роль в приложениях. Иногда и здесь употребляют выражение наиболее вероятное значение случайной величины; это выражение надо понимать не в буквальном смысле ( вероятность любого значения непрерывной случайной величины равна нулю. [12]
Страницы: 1