Критическое значение - параметр
Cтраница 1
Критические значения параметров отмечаются индексом к внизу. [1]
Критические значения параметров, соответствующие переходу от одного состояния к другому, мы называем пределами. [2]
Критические значения параметров устанавливаются путем анализа поведения решения при произвольных малых начальных условиях. [3]
Критические значения параметра Фурье, при которых понижение давления в условиях бесконечного пласта превосходит понижение забойного давления в условиях открытого конечного кругового пласта не более чем на 1 %, приведены в табл. III. [4]
Критические значения параметров потока да0 и Р0 соответствуют случаям, когда а / обращается в нуль. D ( l, ш0, РО, О, Р) обращается в нуль. [5]
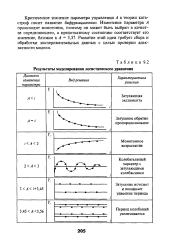 |
Результаты моделирования логистического уравнения. [6] |
Критическое значение параметра управления А в теории катастроф носит название бифуркационного. Развитие этой идеи требует сбора и обработки экспериментальных данных с целью проверки адекватности модели. [7]
Критическое значение параметра порядка S не имеет вполне точного смысла вследствие приближенности / ( 0), но оно оказывается даже больше, чем в решении Онсагера. [8]
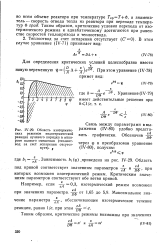 |
Область изотермических режимов эндотермической реакции нулевого порядка в аппарате полного смешения ( теплоот-вод за счет испарения отсутствует. [9] |
Критическим значениям параметров соответствуют обе ветви кривой. [10]
Такие критические значения параметра являются бифуркационными. [11]
Найдены критические значения параметра вдува для гелия азота и углекислого газа при которых тепловые потоки в стенку становятся равными нулю. Предложена физическая модель явления и разработана методика расчета удовлетворительно согласующаяся с экспериментом. [12]
При критических значениях параметров на оси возникает особенность в виде индуцированного стока. Поэтому естественно предположить, что если допускать на оси определенного типа особенности, призванные моделировать, например, турбулентную приосе-вую зону, то решение может быть продолжено в закритическую область. Совместимыми с уравнениями особепостями являются источники жидкости, импульса и момента импульса. В первом и третьем случаях скорость стремится к бесконечности обратно пропорционально расстоянию до оси, а во втором - пропорционально логарифму расстояния. Поскольку особенность, связанная с источником осевого импульса, более слабая, сначала рассмотрим именно этот случай. [13]
При критическом значении параметра Рейнольдса ( Кекр 2320) длина начального участка наибольшая. [14]
Для блок-сополимеров критическое значение параметра Хлв может быть рассчитано по уравнению, предложенному С. [15]
Страницы: 1 2 3 4 5