Верхнее критическое значение

Cтраница 2

На рис. 11.11 представлены результаты для случая кручения с растяжением, сжатием. Верхние критические значения на рис. 11.11 взяты как средние эмпирические. [16]

Коэффициент Дарси при увеличении характеристики шероховатости Ree вследствие изменения скорости уменьшается, приближаясь к своему крайнему значению ЯКв - При уменьшении характеристики шероховатости коэффициент Дарси К должен приближаться к значениям Ягл-Соответственно следует учитывать два критических значения характеристики шероховатости: нижнее ReeH, при котором может установиться движение по типу гладкой области, и верхнее ReeB, при котором устанавливается движение, отвечающее квадратичной ( шероховатой) области. Верхнее критическое значение характеристики шероховатости определяется опытным путем. [17]

Деформация идеальной оболочки при статическом нагружении и безмоментном напряженном состоянии происходит следующим образом. Вначале нагрузка растет до верхнего критического значения Рв ( точка А), затем оболочка совершит скачок ( хлопок) к положению F, после чего нагрузка вновь будет повышаться. Процесс разгрузки происходит вначале по линии DFB и на уровне нижней критической нагрузки происходит скачок по линии BG и снижение нагрузки от точки G до точки О. [18]

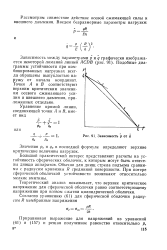Зависимость р от q. [19]

Подобные диаграммы устойчивости при комбинированных нагрузках всегда обращены выпуклостью наружу от начала координат. Точки А и В соответствуют верхним критическим значениям осевого сжимающего усилия и внешнего давления, приложенных отдельно. [20]

Предложенный подход может быть использован и для решения задач устойчивости оболочек в экстремальных условиях температурного и силового нагружения. Дробление приращения силового и температурного нагружения позволяет уточнить верхнее критическое значение нагрузки [9], или критическое значение времени и числа циклов нагружения. [21]

На рис. 20.10 Rt Q / ( 0 8QB), где QB - верхнее критическое значение силы согласно § 1 гл. Имеется большой разброс экспериментальных точек и сильная зависимость кривых взаимодействия от геометрического параметра х - Все это затрудняет рекомендовать какую-либо из кривых взаимодействия. Надежной следует считать прямую линию. [22]

Еще в 1936 г. советский физик Л. В. Шубников, экспериментируя со сверхпроводящими сплавами, обнаружил, что магнитное поле проникает в образец, который частично все еще остается сверхпроводящим. Значение поля, при котором начинается проникновение, получило название нижнего или первого критического магнитного поля с индукцией ЯК1, а при втором - верхнем критическом значении магнитного поля с индукцией Вк2 сверхпроводимость полностью исчезает во всем образце. В промежутке между этими значениями полей эффект Мейснера проявляется не полностью и сверхпроводник находится в особом смешанном состоянии. [23]

Безопасность процесса прямого окисления в кипящем слое катализатора обеспечивается путем создания автоматической стабилизации технологических параметров. Для построения автоматической системы защиты ( АСЗ) процесса приняты шесть информационных параметров, получаемых с помощью автоматических приборов-датчиков: температура оседания кипящего слоя, падение давления сырья, снижение температуры в реакторе ниже оптимальной и превышение верхнего критического значения температуры, превышение критического значения коэффициента избытка воздуха и превышение давления в аппарате. [24]

В турбулентных течениях не удается установить простых выражений внутреннего трения. Приходится обращаться к экспериментам. Рейнольде первый экспериментально определил верхнее критическое значение параметра Re, при котором в трубе устанавливается турбулентное течение, и отметил переходную область между ламинарными и турбулентными течениями. [25]

Однако не все сверхпроводники ведут себя в магнитном поле одинаково. В сверхпроводниках 1-го рода наблюдается эффект Мейссне-ра - Оксенфельда, а в сверхпроводниках 2-го рода проявляется неполный диамагнетизм. Для последних магнитное поле лежит между нижним критическим значением Яс1 ( 7) и верхним критическим значением Яс2 ( 7) напряженности. [26]

При разгрузке две рассматриваемые системы ведут себя также по-разному. Вторая система проходит через новую точку бифуркации В2, где становится неустойчивым отклоненное положение равновесия. В таких случаях точку Вг иногда называют верхней критической точкой, соответствую-щее ей значение нагрузки - верхним критическим значением. [27]

Величина допустимой плотности тока ограничена тем, что ток может разрушить сверхпроводящее состояние, если сила его превысит некоторое критическое для данного сверхпроводника значение / к. Если ток в сверхпроводнике первого рода древысит критический, то сопротивление его становится конечным, и ток начинает идти по всему сечению проводника. В сверхпроводники второго рода ток проникает постепенно, как только сила его станет больше нижнего критического значения, но сопротивление сверхпроводника остается нулевым до тех пор, пока ток не превысит верхнего критического значения. Величина критического тока в сверхпроводниках первого рода пропорциональна величине критической напряженности Як, а в сверхпроводниках второго рода эта зависимость не выполняется. [28]

В разделе 11 о трансзвуковых проблемах докладчик, следуя Тзяну, определяет верхние и нижние критические числа Маха. Нижнее критическое значение соответствует появлению местной скорости, равной скорости звука. Верхнее критическое значение числа Маха соответствует пределу, выше которого неаоз-можно непрерывное течение. Несомненно, такой верхний предел существует для реальной жидкости; не приходится сомневаться в существовании верхнего предела даже для невязкой жидкости, хотя его существование в этом случае, насколько мне известно, строго никогда не было установлено. [29]

Ниже приведены результаты решений задач о выпучивании оболочек за пределами упругости, полученные при рассмотрении устойчивости в малом. В практических расчетах следует пользоваться этими решениями с учетом экспериментальных данных. Эксперименты показывают, что при слабо развитых пластических деформациях необходимо так же, как и в пределах упругости, отличать устойчивость оболочек в малом и в большом. Поэтому рекомендуется при проведении расчетов использовать верхние критические значения нагрузок, умноженные на поправочные коэффициенты, учитывающие возможность выпучивания в большом. Когда пластические деформации значительны, можно вести расчеты лишь на устойчивость в малом. [30]

Страницы: 1 2 3