Среднее арифметическое значение

Cтраница 2

Средние арифметические значения были получены Ibbotson Associates делением суммы всех годовых доходов и дивидендов за 63 года. [16]

Средние арифметические значения v вычисляют для каждого образца, предел прочности образца при ежа-тии R определяют механическими испытаниями. [17]

Среднее арифметическое значение выборки ( выборочное среднее) является наилучшей оценкой для генерального среднего А. Это максимально приближенное к истинному значение включает все неисключенные систематические ошибки, поэтому оно необязательно будет правильным для экспериментатора. [18]

Среднее арифметическое значение обводненности, определяемое по формуле ( 11), характеризует центр тяжести проведения изоляционных работ и успешности. [19]

Среднее арифметическое значение X, являющееся математическим ожиданием определяемой величины. [20]

Средние арифметические значения групп не имеют смещения, если А Атт. [21]

Среднее арифметическое значение погрешности д / - дает обобщенную характеристику погрешности каждого измерения, входящего в ряд. Если погрешность первого измерения составила 0 09 мм, то погрешность седьмого составила - 0 08 мм; есть погрешности, равные 0 01; - 0 05; - 0 02; - 0 03; 0 05 мм и др. В среднем же, можно сказать, что погрешность одного измерения в ряду измерений г 0 04 мм. [22]

Среднее арифметическое значение отсчета, полученное по шкале нижнего предела с поглощающим стеклом, 902 С. [23]

Среднее арифметическое значение жесткости менее 50 гс вычисляют с погрешностью не более 0 01 гс и округляют до ОД гс; 50 гс и более - с погрешностью не более 0 1 гс и округляют до 1 гс. [24]

Поправочный коэффициент В для учета искажения поля у краев электродов. [25]

Найденные средние арифметические значения и принимают за окончательный результат испытаний. [26]

Средние арифметические значения рядов измерений подчиняются нормальному закону распределения, если результаты каждого ряда рассеяны нормально. [27]

Среднее арифметическое значение объемной массы принято исходя из предположения, что температура между данными уровнями будет возрастать по линейному закону. [28]

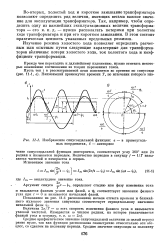Изображение синусоидальной функции. а - в прямоугольных координатах, б - векторное. [29]

Среднее арифметическое значение синусоидальной величины за целый период равно нулю, так как функция расположена симметрично относительно осп абсцисс, со сдвигом на половину периода. [30]

Страницы: 1 2 3 4