Приближенное значение - коэффициент - активность
Cтраница 1
Приближенные значения коэффициентов активности для ионов различного заряда в зависимости от ионной силы раствора сводятся в справочные таблицы; для недиссоциированных молекул f l, так как электростатические взаимодействия между ними отсутствуют. [1]
Находим приближенное значение коэффициентов активности данных ионов. [2]
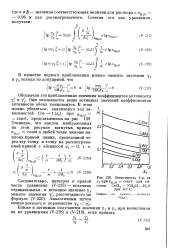 |
Зависимость 1 / m от 22 при аНгО const для системы СоС12 - NH. C1 - Н О при 60 С. [3] |
Обозначим эти приближенные значения коэффициентов активности 7 и - 2 - Они оказываются выше истинных значений коэффициентов активности обоих компонентов. [4]
Вычислив ионную силу раствора, находим по таблице приближенные значения коэффициентов активности / к и / нс. Так как в таблице нет ионной силы, равной 0 017, то / к и / нс4н4оГ находим методом интерполяции. [5]
В настоящее время для аналитических вычислений пользуются таблицей приближенных значений коэффициентов активности. [6]
Вообще говоря, данные по взаимной растворимости позволяют находить только приближенные значения коэффициентов активности, хотя, конечно, лучше хоть такие расчеты, чем никаких. Их результаты чувствительны не только к выбору выражения для gE, но даже и к малым ошибкам эксперимента по определению взаимной растворимости. [7]
Найденные коэффициенты активности ионов вполне согласуются с данными таблицы приближенных значений коэффициентов активности. [8]
Поэтому часто замечалось, что хорошее определение параметров фазового равновесия пар - жидкость для многих систем может быть проведено при использовании только приближенных значений коэффициентов активности, если известны точные значения давлений паров чистых компонентов. Однако в расчетах равновесия жидкость - жидкость небольшие погрешности коэффициентов активности могут привести к серьезным ошибкам. [9]
Температуру находят в первом приближении, применяя закон Рауля к компоненту, находящемуся в большем количестве. Это дает возможность определить приближенные значения коэффициентов активности компонента, присутствующего в меньшем количестве. С помощью графика, построенного в полулогарифмических координатах, находят в первом приближении величины ААВ и АВА. [10]
Страницы: 1