Приближенное значение - скорость
Cтраница 1
Приближенные значения скоростей при минимальном градиенте давления для потока водной суспензии, содержащей - 25 объемн. [1]
Определение приближенных значений скорости резания при продольном точении резцами из быстрорежущей стали производится с помощью графиков, приведенных на фиг. При этом учитывается строение стружки ( сливная или ступенчатая), образующейся при точении данной стали. [2]
Вызовом 2.3 STIT задаем приближенное значение скорости и температуры на ( п 1) - м слое, устанавливаем нулем значение счетчика итераций. [3]
В табл. 46 приведены приближенные значения скоростей горения ряда ВВ при температуре вспышки, полученные экстраполяцией на основании данных для более низких температур, и характеристика поведения ВВ при вспышке. Те вещества, которые имеют скорость горения, превышающую предельное значение, дают взрыв при самовоспламенении, в то время как для веществ с мягкой вспышкой скорость горения много меньше. [4]
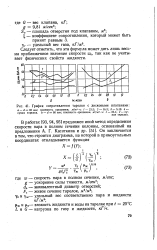 |
График сопротивления тарелки с дисковыми клапанами. [5] |
Следует отметить, что эта формула может дать лишь весьма приближенное значение скорости w0, так как не учитывает физических свойств жидкости. [6]
Здесь, как и в других случаях, пользуясь таблицами, мы находим лишь приближенные значения скорости резания. [7]
В тех случаях, когда кинетические кривые имеют незначительную кривизну вместо начальной скорости, вычисляемой по наклону касательной, можно использовать приближенные значения скоростей, находимые как частное от деления величины ряяног / ги концентраций на входе и выходе реактора на среднее время пребывания. [8]
Расхождение между величинами Qicp и Qscp объясняется как нестационарностью процессов, протекающих в трубопроводе, так и некоторым несовершенством разработанного алгоритма. Приближенные значения скорости и, определяемые выражениями. [9]
При подборе вентилятора поступают следующим образом. Точка А - пересечения этих линий определяет приближенное значение наиболее выгодной скорости УВЫХ з выходном отверстии. [10]
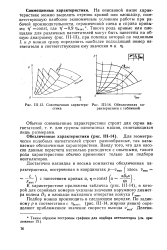 |
Совмещенная характери - [ IMAGE ] - 14. Обезличенная ха-стика рактеристика с табличкой. [11] |
По заданному р в соответствии с т ] мжс ( рис. 111 - 14, жирная линия) определяют приближенное значение скорости выхода с ых. [12]
Теплообмен в трубе прямоугольного сечения с учетом диссипации энергии. Для большинства призматических труб с сечением в виде выпуклого многоугольника, в том числе для прямоугольной трубы, стабилизированное поле скоростей как решение уравнения Пуассона (4.16) не может быть выражено точной аналитической формулой. Поэтому, как было отмечено выше, для решения задач теплообмена в уравнение переноса энергии (4.259) вводятся приближенные значения скорости w ( y, z), найденные различными аналитическими или численными методами. К числу наиболее эффективных аналитических методов относится метод ортогональной проекции Бубнова - Галер-кина. [13]
Вариационные принципы Лагранжа и Кастильяно для задач ползучести являются, очевидно, простой перефразировкой соответствующих принципов для нелинейно упругого тела, поскольку исходная гипотеза состоит в допущении зависимости потенциального типа между напряжениями и деформациями или скоростями деформации. При степенном законе установившейся ползучести с возрастанием показателя п в ряде случаев распределение напряжений мало отличается от того, которое соответствует предельному состоянию идеального жестко-пластического тела. Таким образом, вводится понятие о предельном состоянии ползучести; напряжения сг / для этого состояния находятся по схеме жестко-пластического тела, причем предел текучести зависит от характера нагрузки. Приближенные значения скоростей находятся прямым применением теоремы Кастильяно. [14]
Как известно, существует несколько источников тепловыделения. Если протекает экзотермическая химическая реакция, то, как правило, решается задача о распространении волны при наличии последовательных [228] или независимых [229] реакций. Узость зон реакций, которую часто можно обосновать, например в горении, дает возможность решать задачу в приближении поверхности горения. Такой подход позволяет выявить различные режимы распространения волны, условия их реализации, найти приближенное значение скорости и расстояние между зонами реакций. Так как скорость химической реакции мала при низких температурах, то время выхода на промежуточную асимптотику меньше времени вырождения волны, и волна от превращения второй реакции распространяется по продукту первой реакции. [15]
Страницы: 1 2