Численное значение - корень
Cтраница 1
Численное значение корней в любой точке подобластей 1А и ID обозначено на прямых и кривых, пересекающихся в данной точке. [1]
Численные значения корней указаны в разд. [2]
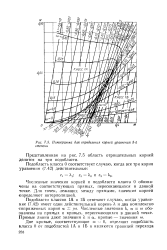 |
Номограмма для определения корней уравнения 3 - й степени. [3] |
Численные значения корней и подобласти класса 0 обозначены на соответствующих прямых, пересекающихся в данной точке. Для точек, лежащих между прямыми, значения корней определяют интерполяцией. [4]
Численные значения корней уравнения ( Б-1-1) мечут быть легко найдены из рассмотрения проведенного на стр. Каждое значение / приводит к бесконечному числу корней и, следовательно, к бесконечному, хотя и дискретному набору уровней энергии. [5]
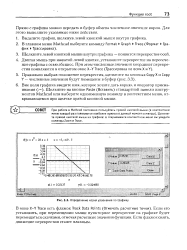 |
Определение корня уравнения по графику. [6] |
Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните указанные ниже действия. [7]
Операция эта не меняет ни характера, ни численного значения корней, потому что отношения коэффициентов между собой остаются без изменения. Но как мы могли только что убедиться, эти соотношения коэффициентов в некоторых случаях нас не могут удовлетворять и желательно иметь возможность их изменить надлежащим образом. [8]
Таким образом, анализ устойчивости сводится к исследованию величины численных значений корней характеристического уравнения. [9]
Если бы мы решали эту задачу классическим способом, то нам, очевидно, пришлось бы получить прежде всего для системы исходное дифференциальное уравнение ( четвертого порядка и, следовательно, с правой частью), найти численные значения корней характеристического уравнения ( для уравнения без правой части), выписать ( судя по их виду) интеграл уравнения без правой части. Затем задаться видом частного решения уравнения с правой частью каким-либо из известных нам методов ( например, методом вариации произвольных постоянных или методом неопределенных множителей Лагранжа), для чего придется многократно ( 3 раза) дифференцировать и, получив общий интеграл, искать постоянные интегрирования. [10]
Выражения 16 - 20 - ограничения типа неравенств, обеспечивающие физический смысл численных значений корней системы. [11]
Мы видели уже, что ниже критической изотермы расположена область равновесия жидкости и пара, где изотермы, построенные по уравнению Ван-дер - Вальса, пересекаются с изобарами, отвечающими равновесию, в трех точках. Здесь, следовательно, для соответственно выбранных значений температуры и давления все три корня рассматриваемого уравнения являются вещественными и неодинаковыми. Близ критического состояния численные значения корней мало отличаются друг от друга, и в критической точке они совпадают. [12]
 |
Изотермы для двуокиси углерода ( площади BFD равны. [13] |
Мы видели уже, что ниже критической изотермы расположена область равновесия жидкости и пара, где изотермы, построенные по уравнению Ван-дер - Ваальса, пересекаются с изобарами, отвечающими равновесию, в трех точках. Здесь, следовательно, для соответственно выбранных значений температуры и давления все три корня рассматриваемого уравнения являются вещественными и неодинаковыми. Близ критического состояния численные значения корней мало отличаются друг от друга, и в критической точке они совпадают. [14]
При этом пособие не касается собственно теории дифференциальных уравнений. Здесь проводится подготовка к анализу устойчивости электрических систем при малых изменениях режима. Применитетьно к этой задаче рассматриваются способы анализа характеристического уравнения без нахождения численных значений его корней ( алгебраические критерии устойчивости, частотные критерии), в связи с этим рассматривается техника нахождения численных значений корней характеристического уравнения. При этом возникает необходимость в решении алгебраических уравнений любого порядка и применении численных методов, позвочяющих находить качественные показатели переходного процесса, оценивающие затухание и частоту вынужденных и свободных колебаний, появившихся в электрической системе после малого возмущения. [15]
Страницы: 1 2