Численное значение - коэффициент - диффузия
Cтраница 1
Численное значение коэффициента диффузии у жидкостей много меньше, чем у газов. [1]
Численные значения коэффициентов диффузии ( в процессах переноса массы целевого компонента), теплопроводности ( для переноса теплоты) и вязкости ( в процессах переноса количества движения при перемещении вязких жидкостей) зависят от свойств среды, в которой происходят соответствующие процессы диффузионного переноса. [2]
Численное значение коэффициента диффузии у жидкостей много меньше, чем у газов. [3]
Подстановка численных значений коэффициентов диффузии и вязкости в выражение ( 8 14) делает очевидным различие чисел Прандтля для газов и жидкостей. [4]
В табл. II-VIII приведены численные значения коэффициентов диффузии, коэффициентов теплопроводности и вязкости. Работы, указанные в заголовках к таблицам, содержат более полные сведения. [5]
Следует отметить, что численные значения коэффициентов диффузии в газах примерно на четыре порядка больше, чем коэффициенты диффузии в жидкостях. [6]
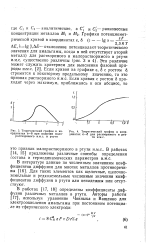 |
Теоретический график в координатах 8 - 6 при наличии малорастворимого и.м.с. в ртути.| Теоретический график в координатах е-б для растворимого в ртути и.м.с. [7] |
Для таких элементов как щелочные, щелочноземельные и редкоземельные численные значения коэффициентов диффузии в ртути или ненадежны или отсутствуют. [8]
Сведения о численных значениях коэффициентов диффузии весьма ограниченны. Особенно мало данных по их экспериментальному определению. [9]
Как было выяснено выше, теория диффузии Френкеля, в которой рассматривается перемещение одного атома во внешнем силовом поле соседних атомов металла, является сильно схематизированной теорией. Однако, если не ставить перед собой задачу определения численных значений коэффициентов диффузии и интересоваться лишь качественными зависимостями их от температуры, а в сплавах еще и от состава, а также параметров, характеризующих размещение атомов разного сорта, то такая теория может быть с успехом применена и к более сложным случаям. При этом, конечно, подразумевается, что температура тела постоянна, неоднородные поля напряжений отсутствуют и тело не имеет неоднородностей, не связанных с наличием градиентов концентраций диффундирующих веществ. Таким образом, предполагается, что отсутствуют причины, приводящие к возможности восходящей диффузии и других явлений, требующих для своего объяснения более общего подхода. Поэтому в дальнейшем модель диффузии Френкеля будет широко применяться при решении различных вопросов указанного типа. [10]
В табл. 44 представлены данные различных работ относительно коэффициента самодиффузии Н2О при Г 25 С. Анализ этих данных показывает, что в пределах точности эксперимента численное значение коэффициента диффузии не зависит от того, каким методом он измерен. [11]
В случае рассмотрения основного уравнения теплопроводности или электропроводности, формально аналогичного уравнению диффузии, так же, как и для диффузии в ненабухающих твердых телах, неизменное в течение всего процесса положение системы координат можно легко и точно определить. Однако для диффузии в жидких смесях и растворах это не так просто. В жидкостях изменение концентрации в результате диффузии приводит к изменениям плотности и объема. Следовательно, неподвижная плоскость, по отношению к которой фиксируется система координат и которая расположена в сосуде, содержащем жидкость ( плоскость, которую можно было бы считать начальной плоскостью диффузии), обычно не может считаться плоскостью отсчета, характеризуемой постоянными физическими параметрами. По существу эти возможности относятся к разным определениям коэффициента диффузии, и поэтому численные значения коэффициента диффузии, установленные для разных систем координат, также различны, хотя различия обычно малы. [12]
Страницы: 1