Минимальное значение - дисперсия
Cтраница 1
Минимальное значение дисперсии дает эффективную оценку. [1]
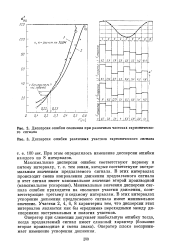 |
Дисперсия ошибки слежения при различных частотах гармонического сигнала.| Дисперсия ошибки различных участков гармонического сигнала. [2] |
Минимальные значения дисперсии сигнала ошибки приходятся на пологие участки движения, соответствующие третьему и седьмому интервалам. В этих интервалах ускорение движения предлагаемого сигнала имеет минимальное значение. Участки 2, 4, 6, 8 характерны тем, что дисперсии этих интервалов являются как бы средними переходными между дисперсиями экстремальных и пологих участков. [3]
Из выражения (5.15) видно, что минимальное значение дисперсии оценки имеет место при таком значении порогового уровня Н / /, при котором крутизна фронта сигнала в точке его пересечения максимальна. [4]
Из выражений (14.9) выбирается п функций, имеющих минимальные значения дисперсий я-критериев. [5]
Реализуемая передаточная функция, соответствующая (16.14), обеспечивает в системе минимальное значение дисперсии ошибки для заданных входных стационарных случайных сигналов в установившемся режиме. [6]
Обычно в качестве наилучшего приближения принимается такое, которому отвечает минимальное значение дисперсии ошибки De. Поэтому проблема оптимизации системы, имеющей своей задачей образование на выходе процесса Z ( t), связанного с X ( t) преобразующим оператором G ( р), сводится к нахождению такой передаточной функции Я ( р), которая обращает в минимум дисперсию ошибки. [7]
 |
Оптимальный линейный фильтр для выделения квазидетерминиро-ванного сообщения. [8] |
Таким образом, на выходе фильтра в точке 3 рис. 7.3.1 в любой момент времени /, в том числе и в момент окончания сигнала tK, обеспечивается минимальное значение дисперсии при данном математическом ожидании. [9]
Большим шагом в совершенствовании процессов получения НК - и МК-отливок была разработанная в ВИАМ под руководством акад. Это обеспечивает минимальные значения дисперсии служебных свойств и максимальную надежность лопаток. [10]
Однако при машинной обработке результатов проверка других возможных моделей с помощью данного метода не составляет особого труда. Отсутствие сходимости с каким-либо минимальным значением дисперсии наблюдалось в случае применения программы DALSFEK только тогда, когда модель была абсолютно неприемлемой. [11]
Разброс значений вычисленных таким образом приведенных расходов воды для достаточно широкой выборки жилых зданий будет тем меньше, чем правильнее будут выбраны численные значения / Сип. Использование этого критерия позволяет обоснованно наложить ограничения на снижение среднего по выборке значения приведенного удельного суточного расхода, чего не удается сделать, если за критерий правильности выбора величин К и п принять минимальное значение дисперсии приведенных расходов волы. [12]
Страницы: 1