Среднегеометрическое значение

Cтраница 4

В 1944 г. Б. С. Стечкин и независимо от него Л. Г. Лойцянский показали, что теорема Жуковского с достаточной для практических целей точностью может быть распространена и на случай обтекания решетки дозвуковым потоком невязкого сжимаемого газа, причем в этом случае Рртда, Г, где Qm 1 / 0102 - среднегеометрическое значение плотности газа в решетке. [46]

Продолжение линии с наклоном - 6 дб / октава до 0 дб определяет значение частоты со. Среднегеометрическое значение между ю0 и coj равняется ш, / 10 3 16, что одинаково с частотой ( йс, при которой линия - 12 дб / октава пересекает ось абсцисс. [47]

Получено среднегеометрическое значение, равное 101 29 мдарси. [48]

В табл. 9.1 приведены поправочные коэффициенты, вычисленные для среднеарифметических значений частот. Аналогичные таблицы составляются и для среднегеометрических значений частот. [49]

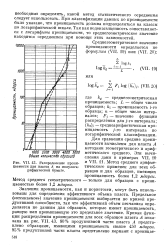Распределение проницаемости для пласта А на полулогарифмической бумаге. [50]

При классификации данных по проницаемости было указано, что проницаемость должна подразделяться на классы по логарифмической шкале. Так как водонасыщенность сопоставляется с логарифмом проницаемости, то среднегеометрическое значение находится осреднением при помощи этих зависимостей. [51]

Лебок 25 на основании измерения вязкости систем из эпоксидных смол и глицидных эфиров, а также аминодиэпоксидов, приходит к выводу, что правило Лейлиха, касающееся взаимодействия между полимером и пластификатором, если его вообще можно рассматривать количественно, выполняется лишь при исключении физического взаимодействия между компонентами системы. Из экспериментальных данных Лебока значение вязко-сти системы не соответствует среднегеометрическому значению вязкостей компонентов. Наличие такого расхождения дает право Лебоку утверждать, что в системе происходит взаимодействие между полимером и пластификатором. [52]

Применение уравне - ний (11.45) - (11.47) приводит обычно к таким же ( если даже не лучшим) результатам, что и использование рис. II. Например, было замечено, что во многих случаях использование среднегеометрического значения ео [ уравнение ( VI. Хотя этот вывод и не всегда справедлив, но он заставляет сомневаться в том, может ли для большинства смесей быть найдено точное значение B - j даже в тех случаях, когда молекулы компонентов малы по величине, неполяр-ны и обладают сферической симметрией. [53]

Нужно отметить, что хотя среднеквадратичное значение тока правильно определяет потери в меди обмоток, оно далеко не всегда достаточно точно определяет повышение температуры обмоток. Если, например, нагрузка в течение длительного времени превышает номинальную, то действительное превышение температуры может значительно превосходить величину, подсчитанную по среднегеометрическому значению тока. [54]

Полинг ввел в 1932 г. понятие электроотрицательности атомов как количественную характеристику способности атома в молекуле притягивать к себе электроны. Он использовал понятие электроотрицательности для объяснения того факта, что энергия гетерополярной связи А-В, которую символически можно обозначить D ( АВ), в общем случае больше среднеарифметического или среднегеометрического значения энергий гомеополярных связей молекул А-А и В-В. [55]

Сравнение тех или иных показателей условий труда с их нормативными значениями позволяет определить индекс соответствия фактических условий труда нормативным. В тех случаях, когда по отдельным факторам условий труда нормативы отсутствуют, следует использовать общесанитарные нормы. В целом уровень организации условий труда на предприятии или в цехе характеризуется коэффициентом условий труда ( KyJ, представляющим собой среднегеометрическое значение индексов соответствия фактических условий труда нормативным. [56]

Распределение потоков в мсжтрубном пространстве при наличии перегородок. [57]

Из нескольких интегральных методов основными являются следующие два. Первый метод [10, 11] применяется для теплообменников без перегородок. Он основан на том, что в критериальном уравнении ( 2) для расчета теплоотдачи используются проходные сечения для потока, представляющие собой среднегеометрические значения между минимальным поперечным проходным сечением пучка труб и проходным сечением продольного потока через свободный сегмент перегородки. [58]

Что же касается Еков, то, в сущности, мы не располагаем удовлетворительным методом ее вычисления. Это объясняется отсутствием каких бы то ни было параллелей с ионными кристаллами, с помощью которых можно было бы получить необходимые численные данные. Грубые оценки, полученные в приближении метода МО, показывают, что постулат о среднеарифметическом значении более приемлем, численные же оценки Полинга и Шермана [302] свидетельствуют в пользу предположения о среднегеометрическом. Следует отметить, что оба они приводят к весьма близким результатам, если энергии А-А и В-В не слишком различаются. Таким образом, обычно разница небольшая, хотя в некоторых случаях ( например, LiH, NaH) среднегеометрическое значение более приемлемо. [59]

Страницы: 1 2 3 4