Низкотемпературное значение

Cтраница 1

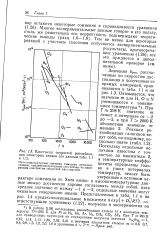Константы скоростей рекомбинации некоторых атомов ( по данным и. [1]

Низкотемпературные значения измерены непосредственно, высокотемпературные рассчитаны по измеренным константам скоростей диссоциации. [2]

В такие низкотемпературные значения энергии активации не нужно вводить поправок на самоохлаждение; эти значения были использованы для вычисления предэкспоненциального множителя, который оказался на 10 или 11 порядков выше нормального значения. Этот результат находится в удовлетворительном согласии с выводами Купера и Гарнера, которые считали, что предэкспоненциальный множитель выше нормального значения на 12 порядков. [3]

В разделе 5.8 эта тема рассматривается несколько подробнее и предлагается методика, которая связывает низкотемпературные значения теплот парообразования с теплоемкостью жидкости. [4]

ДЯ const, могут оказаться гораздо меньше экстраполяции на очень высокие температуры полного уравнения ДЯ / ( Г), полученного на основании низкотемпературных значений теплоемкостей. [5]

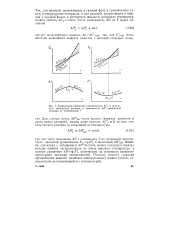Зависимость изменения теплоемкости АС. в результате химической реакции и зависимость АН химической реакции от температуры Т. [6]

Ошибка, связанная с допущением АЯ const, может оказаться гораздо меньше ошибки экстраполяции на очень высокую температуру в полном уравнении АЯг) ( Г), полученном на основании низкотемпературных значений теплоемкостей. Поэтому теплоту сгорания органических веществ ( особенно многоатомных) можно считать относительно не изменяющейся с температурой. [7]

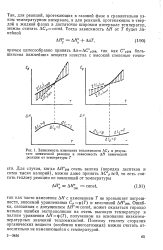Зависимость изменения теплоемкости АСР в результате химической реакции и зависимость ДЯ химической реакции от температуры Т. [8]

Ошибка, связанная с допущением АЯ const, может оказаться гораздо меньше ошибки экстраполяции на очень высокую температуру в полном уравнении АЯт з ( Г), полученном на основании низкотемпературных значений теплоемкостей. Поэтому теплоту сгорания органических веществ ( особенно многоатомных) можно считать относительно не изменяющейся с температурой. [9]

Ошибки, связанные с допущением ДЯ - const, могут оказаться гораздо меньше ошибок экстраполяции на очень высокие температуры полного уравнения ДЯ о ( Т), полученного на основании низкотемпературных значений теплоемкостей. [10]

Все энергии соответствуют низкотемпературным значениям, за исключением EQ для Si, измеренной при комнатной температуре. [11]

Грюнайзена, аГпл ( а - коэффициент расширения) и, наконец, с отмеченным выше фактом единообразия в температурной зависимости теплоемкости. Более вероятным объяснением этого факта является отличие коэффициента электронной теплоемкости при высоких температурах от его низкотемпературного значения. С точки зрения электронной теории металлов это может быть следствием электрон-фононного взаимодействия. Изменения коэффициента электронной теплоемкости у с температурой у тантала, вольфрама и ванадия согласуются с имеющимися в литературе теоретическими оценками. [12]

Зондхеймер [220], используя модель Блоха, рассмотрел отклонения от правила Маттисена для электронной тепло - и электропроводности и составил таблицы, с помощью которых можно находить порядок величины необходимых поправок. Если мы, рассмотрев низкотемпературный предел, определили величину электрического сопротивления, обусловленного примесями, то, согласно правилу Маттисена, эту величину сле дует добавить к сопротивлению чистого металла при всех температурах. В случае электронной теплопроводности необходимо было бы определить предельное низкотемпературное значение WeT, а затем, разделив найденную величину на соответствующую температуру, добавить полученное таким образом значение к идеальному тепловому сопротивлению при любой температуре. [13]

Коэффициенты переноса для многокомпонентного реагирующего частично ионизованного газа определить довольно трудно. На основе обычных металлов кинетической теории был сделан ряд расчетов, однако результаты неодинаковы из-за различных предположений о величине поперечных сечений столкновений. По-видимому, те расчеты, в которых учтены низкотемпературные значения поперечных сечений ( см. [14] или [15]), в настоящее время настолько же верны, как и любые другие расчеты. [14]

Страницы: 1