Истинное среднее значение

Cтраница 2

Для большей достоверности исследований прибор 3 раза останавливают на одних и тех же глубинах, принимая за истинные средние значения. Это особенно важно для дебитомеров с пакером фонарного типа. Необходимость трехкратных замеров обусловлена непостоянством коэффициента пакеровки. При исследовании скважины дебитомером с металлическим пакером типа ДГД-4 проводить повторные замеры на одной и той же глубине невозможно, поэтому измерения следует делать через небольшие интервалы, равные 20 - 30 см. Большое число замерных точек повышает надежность исследований. [16]

Пусть i ( 9) означает вероятность того, что последовательный критерий приведет к принятию партии, когда 6 - истинное среднее значение. [17]

Найденный объем выборки определяет заданную максимально возможную относительную погрешность, которую мы допустим, принимая среднее значение параметра по данным выборки х за истинное среднее значение. [18]

Ведь различные значения случайной величины могут иметь различные вероятности, и поэтому более вероятные значения будут чаще встречаться на практике и в большей мере определять истинное среднее значение случайной величины. Поэтому для оценки среднего ( в вероятностном смысле) значения случайной величины вводится понятие математического ожидания, представляющего собой действительно среднее значение случайной величины, определяемое с учетом различных вероятностей отдельных значений. [19]

Величина п из формулы ( 3), полученная путем усреднения результатов по серии из N опытов, конечно, тоже не вполне точно совпадает с истинным средним значением па и сама является случайной величиной. [20]

Если мы будем иметь 100 выборок и выполним для каждой из них указанные выше расчеты, то можно ожидать, что в 95 случаях внутри полученных пределов будет находиться истинное среднее значение совокупности. [21]

Положение неизвестного среднего значения определено, и в этом случае нельзя говорить о его вероятности. Истинное среднее значение находится или внутри указанной области распределения средних значений, или вне ее. Можно говорить только о вероятности правильности нашего предположения, что средняя находится в данном интервале изменения. Вероятность 90 % означает, что если бы мы изо дня в день по указанному выше методу подсчитывали величины интервалов, в которых должна находиться средняя, и каждый раз путем полного исследования определяли распределение действительного среднего значения, то в 90 % всех случаев наше предположение было бы правильным, а в 10 % истинное среднее значение находилось бы вне указанных границ. [22]

Энтальпию жидкости на стенке Аот определяем как сумму из энтальпии насыщения и теплоты перегрева. Энтальпию жидкости в ядре потока определяем через истинное среднее значение паросодержания в данном сечении. [23]

У, который все же может дать некоторую информацию о процессе кристаллизации. Определенная таким образом величина 0 равна или меньше истинного среднего значения свободной энергии поверхности раздела, ибо не учитывается неоднородная нуклеация и возможность снижения скорости вторичной нуклеации. [24]

Это среднеарифметическое значение близко к математическому ожиданию, т.е. к истинной средней вечичине, и может быть с достаточной степенью точности приравнено к среднему значению случайной величины. При единичных измерениях значений случайной величины их среднеарифметическое значение может существенно отличаться от истинного среднего значения. [25]

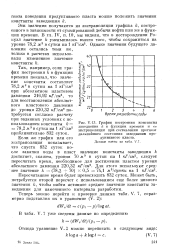График построения константы заводнения k в функции времени и е экстраполяции при составлении прогноза дальнейшего состояния заводнения продуктивного пласта. Данные взяты из. [26]

Может быть, потребуется второй пересчет с использованием еще более низкого значения k, чтобы найти истинное среднее значение константы заводнения для намеченного интервала разработки. [27]

В главе 7 подробно описываются достижения Якоба Бернулли. Закон больших чисел, по существу, утверждает, что различие между средними значениями величин, наблюдаемыми в выборке, и истинным средним значением по всей совокупности будет уменьшаться при увеличении объема выборки. [28]

Важную роль в статистике играют и другие распределения вероятностей. Среди них можно, в частности, назвать 1) / - распределение Стьюдента, полезное в статистических выводах и при вычислении доверительных интервалов для истинных средних значений; 2) F-распределение, которое используется при проверке на равенство пар средних квадратов. [29]

Описанный выше способ определения производительности котла или теплопотребления технологических аппаратов является приближенным и, разумеется, не может претендовать на высокую точность. Однако этот способ дает достаточно точные для производственных условий результаты, но не может быть применен при ламинарном режиме течения теплоносителя, так как в этом случае замеряемая температура теплоносителя не отражает ее истинных средних значений. Однако можно показать, что в установках с дифенильной смесью движение конденсата в трубопроводе всегда имеет турбулентный характер, и поэтому для-этих установок всегда может быть применен рассматриваемый способ определения теплопроизводительности котла. Действительно, в установках с дифенильной смесью скорость теплоносителя в трубопроводах принимается 0 8 м / сек при принудительной и 0 3 м / сек при естественной циркуляции во внешнем контуре. Диаметр магистрального трубопровода обычно принимается не менее 50 мм. [30]

Страницы: 1 2 3