Взаимодействие - ядерный момент
Cтраница 1
 |
Квадрупольное расщепление. [1] |
Взаимодействие ядерных моментов с моментами электронной оболочки приводит к сверхтонкому расщеплению энергетических уровней ядра. Характер и величина этого расщепления определяются распределением электронной плотности в том соединении, в состав которого входит атом. [2]
Взаимодействие ядерных моментов с электронными создает общую систему уровней; в этой системе уровней можно выбрать переходы, насыщение к-рых позволяет полу-нить увеличение поляризации ядер. [3]
Наконец, определенный вклад в сверхтонкое расщепление молекулярных уровней дает эффект взаимодействия ядерного момента с вращением молекулы. Вращающаяся молекула, как движущаяся система зарядов, создает определенное магнитное поле; это поле может быть вычислено с помощью известных из электродинамики формул по заданной плотности тока j р [ Иг ], где р - плотность зарядов ( электронов и ядер) в неподвижной молекуле, а И - угловая скорость ее вращения. Величина расщепления уровней получается как энергия магнитного момента ядра в этом поле, причем компоненты угловой скорости молекулы должны быть выражены через компоненты ее момента ( ср. [4]
Наконец, определенный вклад в сверхтонкое расщепление молекулярных уровней дает эффект взаимодействия ядерного момента с вращением молекулы. Вращающаяся молекула, как движущаяся система зарядов, создает определенное магнитное поле; это поле может быть вычислено с помощью известных из электродинамики формул по заданной плотности тока j p flr, где р - плотность зарядов ( электронов и ядер) в неподвижной молекуле, а П - угловая скорость ее вращения. Величина расщепления уровней получается как энергия магнитного момента ядра в этом поле, причем компоненты угловой скорости молекулы должны быть выражены через компоненты ее момента ( ср. [5]
Наконец, определенный вклад в сверхтонкое расщепление молекулярных уровней дает эффект взаимодействия ядерного момента с вращением молекулы. Вращающаяся молекула, как движущаяся система зарядов, создает определенное магнитное поле; это поле может быть вычислено с помощью известных из электродинамики формул по заданной плотности тока j p Sir, где р - плотность зарядов ( электронов и ядер) в неподвижной молекуле, a S1 - угловая скорость ее вращения. Величина расщепления уровней получается как энергия магнитного момента ядра в этом поле, причем компоненты угловой скорости молекулы должны быть выражены через компоненты ее момента ( ср. [6]
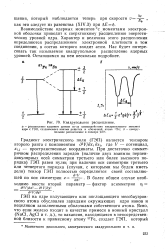
О втором члене гамильтониана мы уже говорили при обсуждении ЯМР: он описывает взаимодействие ядерного момента атома водорода с магнитным полем. Совместное влияние первых двух членов уравнения (9.4) на энергии спиновых состояний атома водорода в магнитном поле показывает рис. 9.2 В. В приведенном примере напряженность магнитного поля фиксирована и штриховые линии показывают изменения энергии, вызываемые введением нового члена в гамильтониан. [7]
При наличии в молекуле тяжелых атомов сравнимый вклад в сверхтонкое расщепление вносит, наряду с прямым, также и непрямое взаимодействие ядерных моментов через посредство электронной оболочки. С формальной точки зрения это взаимодействие представляет собой эффект второго приближения теории возмущений по отношению к взаимодействию ядерного спина с электронами. С помощью результатов § 121 легко найти, что отношение величины этого эффекта к эффекту прямого взаимо - действия ядерных моментов порядка ( 2е2 / йс) а; при больших Z оно сравнимо с единицей. [8]
При наличии в молекуле тяжелых атомов сравнимый вклад в сверхтонкое расщепление вносит, наряду с прямым, также и непрямое взаимодействие ядерных моментов через посредство электронной оболочки. С формальной точки зрения это взаимодействие представляет собой эффект второго приближения теории возмущений по отношению к взаимодействию ядерного спина с электронами. С помощью результатов § 121 легко найти, что отношение величины этого эффекта к эффекту прямого взаимодействия ядерных моментов порядка ( Ze2 / Hc) 2 ] при больших Z оно сравнимо с единицей. [9]
 |
Схема расщепления.| Векторная модель атома в сильном внешнем магнитном поле. [10] |
Так как ядерный и электронный магнитные моменты прецессируют в магнитном поле с разной частотой и как правило в разном направлении, величина энергии W / j взаимодействия ядерного момента с электронной оболочкой также изменится. [11]
Оказывается, что в разных органических молекулах частота протонного резонанса v меняется в интервале примерно 600 гц. Однако на самом деле это заметная величина, так как из-за слабости взаимодействия ядерных моментов друг с другом и с электронными оболочками атомов ширина линий в этом спектре поглощения будет исключительно малой. Несмотря на то что вещества изучаются в жидкости ( а не в газе), ширина линий в них часто не достигает 1 гц. Поэтому интервал в 600 гц, в котором разыгрываются все события, не является столь малым. У азота, йода и других атомов характер спектра более сложен, так как он содержит несколько линий ( мультиплет), но в принципе все будет обстоять точно так же. [12]
Оказывается, что в разных органических молекулах частота протонного резонанса v меняется в интервале примерно 600 гц. Однако на самом дело это заметная величина, так как пз-за слабости взаимодействия ядерных моментов друг с другом и с электронными оболочками атомов ширина линий в этом спектре поглощения будет исключительно малой. Несмотря на то что вещества изучаются в жидкости ( а не в газе), ширина линий в них часто не достигает 1 гц. Поэтому интервал в 600 гц, в котором разыгрываются все события, не является столь малым. У азота, йода и других атомов характер спектра более сложен, так как он содержит несколько линий ( мультиплет), но в принципе все будет обстоять точно так же. [13]
Результат отличается от предыдущего примерно на две десятитысячных. Оно является следствием относительного движения электрона и нуклонов в дейтроне. Сверхтонкое расщепление измеряет взаимодействие ядерного момента с электронным током, а не с внешним однородным полем. Когда электрон при своем движении подходит близко к ядру, то центром плотности вероятности его распределения является не центр тяжести ядра, а центр заряда протона. При этом быстрое и почти сферически-симметричное движение нейтрона вокруг протона приводит к исчезновению любого магнитного действия нейтрона на электрон, когда последний находится внутри нейтронной орбиты. Следовательно, действие отрицательного магнитного момента нейтрона будет уменьшено и эффективный момент дейтрона в электронно-дейтрон ном взаимодействии возрастет. [14]
Страницы: 1