Логарифмическая анаморфоза
Cтраница 3
 |
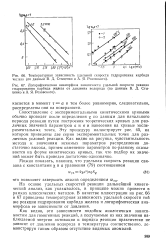
Разновидности частотных характеристик объекта с самовыравниванием. [31] |
Упрощенный анализ динамических свойств систем возможен с помощью логарифмических частотных характеристик, которые представляют собой те же графики зависимостей - j ( со) и ф ( ( о), но только в логарифмической анаморфозе. [32]
В логарифмической анаморфозе гиперболы изолинии мощности преобразуются в прямые линии. [33]
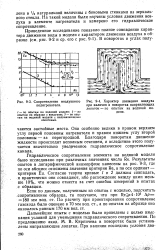 |
Сопротивление воздушного подогревателя.| Характер движения воздуха при наличии в поворотах направляющих лопаток - по опытам на водяной модели. [34] |
Гидравлическое сопротивление элемента на водяной модели было исследовано при различных значениях числа Re. Результаты опытов в логарифмической анаморфозе нанесены на рис. 9 - 3, где по оси абсцисс отложены значения критерия Re, а по оси ординат - критерия Ей. Согласно теории кривые / и 2 должны совпадать, и практически они совпадают, ибо расхождение между ними меньше 10 %, что можно отнести за счет ошибок измерений в опытах с образцом. [35]
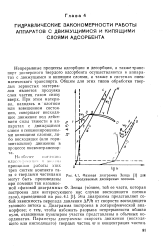 |
Фазовая диаграмма Зенца для продуваемых дисперсных потоков. [36] |
Эта диаграмма представляет собой зависимость перепада давления AP / ft от скорости восходящего газового потока и. Диаграмма построена в логарифмической анаморфозе; с тем, чтобы избежать разрыва непрерывности вблизи нуля, отделенные пунктиром участки представлены в обычных координатах. [37]
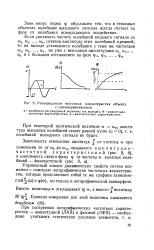
Теперь мы располагаем всеми необходимыми данными для построения графика сопоставления тепловой эффективности рассматриваемых пучков. Задачэ упрощается тем, что в логарифмической анаморфозе зависимость Ef ( AN0) выражается прямой линией: при фиксированных параметрах теплоносителя ( давление, средняя температура) и геометрии пучка как коэффициент теплоотдачи а, так и энергетические затраты на перемещение теплоносителя ANo являются степенными функциями скорости потока. Поэтому для построения зависимости Ef ( AN0) необходимо вычислить по две пары сопряженных значений Е и AN0 для каждой из сопоставляемых поверхностей. [38]
Ясно, что коэффициент сопротивления является функцией критерия Рейнольдса. Рассмотрение графика этой функции, представленного в логарифмической анаморфозе ( рис. 5), приводит к следующим заключениям. [39]
Если отсчитывать все отклонения от среднего, то для восьмой зоны большая их часть даст отрицательную бесконечность в логарифмической анаморфозе и очень малые величины в обычном изображении. Если же отсчитывать отклонения от медианы, то в логарифмической анаморфозе часть их даст неопределенность вида оо - оо, а остальные выразятся положительной бесконечностью. [40]
Так как большинство кривых удовлетворяется уравнениями степенных функций, то можно воспользоваться этим свойством, и коррелировать не непосредственно величины, а их логарифмы. Тогда мы получим не криволинейную, а прямолинейную корреляцию, следовательно, уравнение прямой регрессии логарифмической анаморфозы. [41]
В других случаях эта зависимость может отыскиваться способом наименьших квадратов, а иногда с применением логарифмической анаморфозы. Но все аналогичные примеры охватывают область отыскания по данным измерений эмпирических ( всегда тем самым и приближенных) зависимостей между измеряемыми величинами. [42]
Когда имеем дело с величинами, измеряемыми настолько точно, что их ошибками можно практически не интересоваться, то операция логарифмирования, по существу, ничего не изменяет в математической форме зависимости между двумя ( и более) величинами. Но когда эти ошибки велики и могут влиять ( и даже сильно) на форму отыскиваемой зависимости, то логарифмическая анаморфоза может значительно исказить все соотношение между размером самой измеряемой величины и размерами ошибок ее измерения. [43]
В качестве иллюстрации на рис. 66 и 67 приведены температурная зависимость удельной скорости той же реакции гидрирования карбида железа и логарифмическая анаморфоза ее зависимости от давления. [45]
Страницы: 1 2 3 4