Интерференционное взаимодействие
Cтраница 1
Интерференционное взаимодействие двух резонаторов превращает исходную монохроматическую частоту v в дублет v Av. Эти интерференционные явления - измененную собственную частоту колебаний и периодическую перекачку ( обмен) энергии от одного резонатора к другому - легко наблюдать на опыте с двумя связанными маятниками. [1]
В результате интерференционного взаимодействия между дифрагированными лучами, зависящего от периода решетки, область когерентности определяется не шириной решетки, а ее периодом. [2]
Для получения интерференционного взаимодействия двух колебаний необходимо, чтобы разность фаз была, например, постоянна в течение времени, необходимого для фиксирования результата этого взаимодействия. [3]
Проследим за интерференционным взаимодействием волн на границах расширения и перераспределением энергии в момент резонансного отражения. [4]
При этом благодаря интерференционному взаимодействию излучений формировалась более острая, чем у полуволновых вибраторов, результирующая диаграмма аиравлен-ности. Эта диаграмма для случая линейки представляется формулой F ( Q) Fi ( Q) Fn ( Q), где / 4 ( 6) - диаграмма направленности одиночного излучателя, входящего в состав линейки, a Fn ( 9) - множитель линейки. [5]
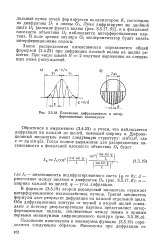 |
Положение дифракционных и интерференционных максимумов. [6] |
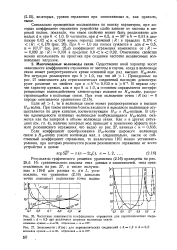
В формуле (3.5.19) второй косинусный множитель отражает интерференционное взаимодействие пучков. Третий множитель формулы дает результат дифракции на каждой отдельной щели. [7]
Таким образом, мы можем считать доказанным первое из высказанных нами в начале предыдущего параграфа утверждений, что физической основой статистики Бозе-Эйнштейна является предположение об интерференционном взаимодействии молекул идеального газа. В высшей степени вероятно, что и второе из высказанных нами утверждений также окажется вполне справедливым и что, стало быть, при учете интерференционного взаимодействия молекул результаты теории Бозе-Эйнштейна будут получены на основе классической статистики без отказа от индивидуализации молекул. Порукой этому служит хотя бы только что упомянутый вывод формулы флуктуации ( 33) из теории де Бройля. К сожалению, общего доказательства этого утверждения пока еще никем не было дано; однако очень интересный шаг в этом направлении удалось недавно сделать Ланде [9], к краткому изложению работы которого мы теперь и перейдем. [8]
Сомножитель sin2 ы / и2 описывает явление дифракции; на одной щели, сомножитель cos2 v характеризуют двухлучевую-интерференцию, создаваемую лучами от каждой щели в результате интерференционного взаимодействия. [9]
При интерференции световых колебаний возникает сложение волн, при котором интенсивность результирующей световой волны в зависимости от разности фаз складывающихся колебаний может быть больше или меньше суммы интенсивностей этих волн. Для получения интерференционного взаимодействия двух колебаний необходимо наличие постоянной разности фаз в течение времени, необходимого для фиксирования результата этого взаимодействия. [10]
Ну, а если подать пять потоков информации сразу в оба полушария: слова в оба уха, написание слов одновременно двумя руками и расположение шахматных фигур, то, несмотря на кажущуюся простоту задачи, мозг с ней не справляется. И не справляется именно в силу возникновения множественных интерференционных взаимодействий. [11]
В предыдущих параграфах рассмотрены случаи, когда при определенных условиях плоская волна могла полностью отражаться от полупрозрачных решеток различных типов. Это явление, обычно носящее ярко выраженный резонансный характер, обусловлено интерференционным взаимодействием полей за решеткой, порожденных различными волнами внутри щелей. [12]
Существенно иной характер носят зависимости коэффициента отражения от частоты в случае, когда в волноводе связи может распространяться кроме основной еще ряд высших / / - волн. В первом случае характер кривых, как и при А 1 0, в основном определяется интерференционным взаимодействием элементарных изломов по / / 10-волне, распространяющейся в волноводе связи. [14]
Таким образом, мы можем считать доказанным первое из высказанных нами в начале предыдущего параграфа утверждений, что физической основой статистики Бозе-Эйнштейна является предположение об интерференционном взаимодействии молекул идеального газа. В высшей степени вероятно, что и второе из высказанных нами утверждений также окажется вполне справедливым и что, стало быть, при учете интерференционного взаимодействия молекул результаты теории Бозе-Эйнштейна будут получены на основе классической статистики без отказа от индивидуализации молекул. Порукой этому служит хотя бы только что упомянутый вывод формулы флуктуации ( 33) из теории де Бройля. К сожалению, общего доказательства этого утверждения пока еще никем не было дано; однако очень интересный шаг в этом направлении удалось недавно сделать Ланде [9], к краткому изложению работы которого мы теперь и перейдем. [15]
Страницы: 1 2