Вид - матрица
Cтраница 1
Вид матрицы, возвращаемой этими функциями, совпадает с возвращаемой функцией rkfixed. Однако функции Stiffr и Stiffb требуют дополнительно задания Якобиана системы уравнений. [1]
Вид матрицы обсуждается в гл. [2]
Вид матрицы р зависит от характера аппроксимации перемещений и будет определен ниже. [3]
Вид матрицы, описанный в этом предложении, назовем упрощенным видом. Матрицы такого вида коротко назовем упрощенными. [4]
Вид матрицы N зависит от выбора независимых замкнутых контуров и принятых направлений их обхода. При одной и той же нумерации узлов и ветвей в зависимости от выбора независимых контуров получаются различные матрицы. [5]
Вид матриц Джонса для данного элемента зависит от ориентации осей координат. [6]
Вид матрицы коэффициентов распределения зависит от порядка нумерации узлов и ветвей. В случае разомкнутой схемы удобно так пронумеровать ветви и независимые узлы, чтобы одна из ветвей, соединенных с каждым узлом, имела тот же номер, что и данный узел. [7]
Такой вид матрицы удобен для записи результатов эксперимента, однако смысл индексов ее элементов ( первый индекс - номер столбца, второй - номер строки) отличается от общепринятого. [8]
Записать вид матрицы рассеяния (10.29) применительно к очень тонкому кристаллу в первом приближении. Как (10.29) тогда связано с кинематическим приближением и с приближением фазовой решетки. [9]
Установим вид матрицы акустоуп-ругих коэффициентов волн Рэлея. [10]
Из вида матриц S1 ( a), B ( a) и невырожденности матрицы В ( а) вытекает следующее утверждение. [11]
Из вида матриц непосредственно вытекает, что это линейное представление имеет приведенную форму. [12]
Из вида матриц непосредственно вытекает, что это линейное представление имеет приведенную форму. Оно дает два линейных представления первого порядка, определяемых числами е - 1й и ем. [13]
По виду матрицы переходных вероятностей определить период d соответствующей цепи Маркова и выделить соответствующие циклические подклассы. [14]
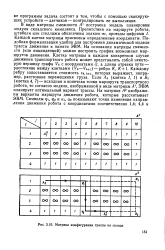 |
Матрица конфигурации трассы на складе. [15] |
Страницы: 1 2 3 4