Качественный вид

Cтраница 1

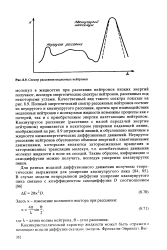Спектр рассеяния медленных нейтронов. [1]

Качественный вид такого спектра показан на рис. 8.9. Полный энергетический спектр рассеянных нейтронов состоит из неупругого и квазиупругого рассеяния, причем при взаимодействии медленных нейтронов с молекулами жидкости возможны процессы как с потерей, так и с приобретением энергии налетающим нейтроном. Квазиупругое рассеяние ( рассеяние с малой передачей энергии нейтроном) проявляется в некотором уширении падающей линии, изображенной на рис. 8.9 штриховой линией, и обусловлено наличием в жидкости низкоэнергетических диффузионных движений. Неупругое рассеяние нейтронов обусловлено обменом энергией с квантованными движениями, которыми являются заторможенные вращения и заторможенные трансляции молекул, т.е. колебательные движения молекул жидкости в поле их соседей. [2]

Качественный вид ф унк ий ipi ( x), i) 2 ( x) и tya ( x) показан на put. Из рисунка следует, что волнов & я функрия не равна нулю и внутри барьера, а в области 3, если барьер не б чень широк. Следовательно, получили, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины. [3]

Качественный вид D-разбиения плоскости параметров ц, v в рассматриваемом случае совпадает с видом D-разбиения плоскости параметров а, р ( см. фиг. Точкам пересечения кривой D-разбиения и С-кривой на диаграмме соответствуют значения со и х 0, первое из которых является частотой возбуждения колебаний ( при переходе из области устойчивости в область неустойчивости), второе определяет положение резца, при котором начинается возбуждение. [4]

Аппарат для сварки пластиката. 1 - пластикат, 2 -электрод, 3 -тележка, 4 - сваренный шов. [5]

Более производительным и качественным видом сварки пластиката является высокочастотная сварка. Для выполнения такой сварки применяют высокочастотную установку ЛГД-1, преобразующую обычный переменный ток в высокочастотный, сварочный аппарат на тележке СПП-2 или ручной аппарат СППР. [6]

В качественном виде указанные соображения применимы также к общему случаю сильного гравитационного поля. [7]

В качественном виде эти процессы представляются следующим образом. По мере вспенивания происходит увеличение размеров ячеек и уменьшение толщины стенок ГСЭ ( см. гл. В результате разрыва стенок образуются сообщающиеся ячейки, наличие которых благоприятствует истечению и улетучиванию газа из вспениваемой массы. Общее количество газа в системе определяется процессами десорбции ( газовыделения) и истечения газа из изделия. По мере снижения температуры и повышения степени вулканизации материала эти процессы замедляются, а затем практически прекращаются. [8]

Хотя в качественном виде эти элементарные акты ясны, но уравнений, описывающих их не существует. [9]

Таким образом, качественный вид структур нормальных ионизующих ударных волн, наблюдаемых в электромагнитных ударных трубах, определяется происходящими в прекурсорной области процессами ионизации и нагрева плазмы. Описание этих процессов требует привлечения кинетических или, на модельном уровне, трехжидкостных гидродинамических уравнений. Уже применение уравнений двухжидкостной гидродинамики приведет к теоретическим структурам, резко отличающимся по виду от наблюдаемых. Что же касается газодинамического приближения в теории ударных волн, в котором прекурсорные явления вообще не учитываются, то оно тем более неадекватно. Поэтому в данном случае неприменимо и приближение, основанное на гипотезе Чепмена - Жуге. [10]

Автомобильный транспорт расходует наиболее качественный вид энергии. [11]

В различных растворителях качественный вид спектра комплексов сохраняется, однако при каждой температуре полоса комплекса в Кг и Хе расположена при меньших частотах и имеет большую полуширину. [12]

Отметим, что качественный вид графиков зависимости сверхтонкого расщепления от ориентации ( рис. 7 - 6) указывает на сравнительно большие значения недиагональных членов. Если же АХу сравнительно велик, то кривая существенно сместится. Хороший пример для этого случая дает рис. 7 - 6, а, тогда как рис. 7 - 6, б соответствует малому Аху. [13]

На рис. 7.2 дан качественный вид этой диаграммы. [14]

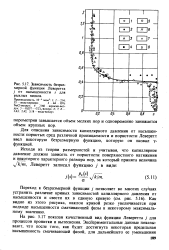Зависимость безразмерной функции Леверетта j от насыщенности. s для рыхлых песков. [15]

Страницы: 1 2 3 4