Адача

Cтраница 1

Адачи подчеркивает, что современный конструктор использует все знания в области разрушения помимо собственного опыта, связанного с определенным видом оружия. Большинство практических проблем артиллерийского вооружения связаны с такими факторами, как, например, остаточные напряжения, долговечность и упругопластичное поведение материала. Поэтому последние достижения механики линейно-упругого разрушения используются лишь в качестве руководства для предварительного выбора геометрических параметров или изменения конструкции на ранних стадиях проектирования. Испытания на выносливость остаются основным критерием для определения долговечности. [1]

Формула Адачи лучше всего подходит к простым случаям, когда преломляющие границы плоские, нет никаких скоростных или структурных аномалий и преломляющие границы залегают на небольшой глубине. Когда перечисленные условия не выполняются, эта формула наряду с другими ей подобными может представлять лишь ограниченный интерес. Часто нельзя с уверенностью считать, что формулы применимы к конкретной реальной ситуации. [2]

В & адачах 792 - 812 найти производные функций у, заданных неявно. [3]

Перед работниками бурения возникает постоянная адача экономии утяжелителя. [4]

Итак, для решения адачи надо найти и - 1 неизвестное. [5]

Приближенное решение одной краевой i адачи для дифференциального уравнения второго порядк i II ПММ-1955 - Т, 19, вып. [6]

Ал гор шм решения группы адач о а. [7]

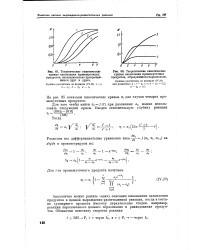Теоретические кинетические. кривые накопления промежуточных продуктов, последовательно превращающихся друг в друга. [8]

Аналогично можно решить Е: адачу описания кинематики накопления продуктов в цепной вырожденно-разветвленной реакции, когда в составе суммарного процесса имеются параллельные стадии, например, реакции параллельного цепного образования и расходования продуктов. [9]

В аналитической геометрии часто рассматриваются две адачи: 1) по заданным геометрическим свойствам кривой составить ее уравнение; 2) по заданному уравнению кривой выяснить ее геометрические свойства. [10]

Дело а том, что при решении адач в иакетнгм режиме вмешательство человека а вычислительный процесс минимально и зга проблема решается много проще. [11]

Случай полного поглощения примеси на берегу соответствует в краевой адаче заданию нулевой концентрации примеси на границе, а случай полного отражения заданиюв краевой задаче нулевого потока примеси на границе. [12]

Здесь мы рассмотрим три достаточно типичные, хотя и простые адачи. Их простота приводит к тому, что во всех трех случаях для нахождения оптимума достаточно применения обычного метода дифференциального исчисления. [13]

Как известно [1], в этом случае должна решаться адача плоской деформации. Обозначим через а половину шири -: ы наименьшего поперечного сечения образца, г0 - радиус кривиз-ы у основания выточки, t - глубину выточки. Решение ведется в: рямоугольных координатах х, у и г. Ось х направим вдоль оси об - ззца, а ось у - в плоскость образца. Метод решения полностью овпадает с изложенным выше для глубокой выточки. [14]

На третьей ступени решаются технические и в основном экономические з адачи. Планируется производство отдельных цехов и участков, выполняются учетные работы, осуществляется управление транспортом, складами, энергоресурсами, определяются показатели для оперативного управления, которые передаются в соответствующие системы автоматики второй ступени. Здесь применяются системы сбора информации о работе основных и вспомогательных производств и вычислительные машины для анализа деятельности всего предприятия, планирования, учета, оперативного управления и выдачи необходимой отчетной документации. В замкнутых системах, кроме того, выдаются управляющие сигналы для заданий планов и режимов работы отдельным производствам. [15]

Страницы: 1 2 3 4