Изменение - физическая величина
Cтраница 1
 |
Пример входного воздействия и отклика на выходе средства измерений. [1] |
Изменение физической величины во времени называется процессом. Процесс может характеризоваться постоянными параметрами. У синусоидального напряжения или тока, например, такими параметрами являются амплитуда, частота, начальная фаза. Их измерение к динамическим не относится. [2]
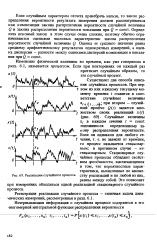 |
Реализации случайного процесса. [3] |
Изменение физической величины во времени, как уже говорилось в разд. [4]
 |
Пример входного воздействия и отклика на выходе средства измерений. [5] |
Изменение физической величины во времени называется процессом. Процесс может характеризоваться постоянными параметрами. У синусоидального напряжения или тока, например, такими параметрами являются амплитуда, частота, начальная фаза. Их измерение к динамическим не относится. [6]
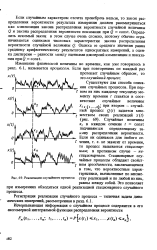 |
Реализации случайного процесса. [7] |
Изменение физической величины во времени, как уже говорилось в разд. [8]
Изменение физической величины, используемое для передачи данных. [9]
Изменение физической величины вдоль любого направления случайного поля аналогично случайному процессу с той лишь разницей, что роль времени играет пространственная координата. Оно задается соответствующими многомерными функциями распределения вероятности физической величины. [10]
Расчет изменения физических величин в косой ударной волне по формулам ( 46 7) - ( 46 12) сопряжен с большими вычислительными трудностями. Поэтому был предложен ряд диаграмм и графических методов, облегчающих эти расчеты. [11]
Для определения характера изменения физической величины с течением времени нужно построить, используя оператор Гамильтона и оператор данной величины, оператор производной, а для него найти среднее в соответствующем состоянии. [12]
Сигнал, в котором изменение физической величины, используемой для передачи, происходит непрерывным образом: в случае передачи информации - в соответствии со значением физической величины той же или другой природы; в случае передачи команды - в соответствии с уровнем требуемого воздействия. [13]
Несмотря на случайный характер изменения физической величины, между ее значениями при различных значениях аргумента ( например, при различных значениях времени или в различных точках пространства) существует определенная связь. Для оценки этой взаимосвязи применяется корреляционная, или автокорреляционная, функция. [14]
Задача заключается в описании изменения физических величин, характеризующих свойства полимеров, при этом преобразовании масштаба. [15]
Страницы: 1 2 3 4