Аддитивность - дисперсионная сила
Cтраница 1
Аддитивность дисперсионных сил проявляется в адсорбции и других процессах, связанных с конденсацией газа. [1]
Вследствие аддитивности дисперсионных сил энергия взаимодействия между макроскопическими телами убывает с расстоянием значительно медленнее, чем между отдельными молекулами. Так, для плоскопараллельных пластин при расстояниях R 100 нм с учетом запаздывающих сил энергия взаимодействия пропорциональна R-3. Когда R соизмерим с межатомными расстояниями, возникает необходимость учета электростатических взаимодействий между полярными элементами структуры твердого тела. При соприкосновении и перекрывании электронных орбиталей поверхностных атомов сближающихся частиц становится заметным вклад близкодействующих сил и в тем большей степени, чем меньше R, что сопровождается или броуновским отталкиванием, или образованием валентных связей. [2]
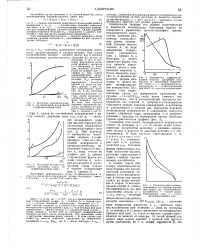 |
Потенциальные кривые, полученные из изотерм адсорбции паров для тонкопористых адсорбентов. 1 - сильно адсорбирующийся нар. 2 - слаОЧе адсорбирующийся пар. [3] |
В тонких порах благодаря аддитивности дисперсионных сил адсорбционный потенциал повышен; о его распределении в объеме пор можно судить по форме изотермы А. [4]
Но мы не подвергаем специальному обсуждению условия суммирования рядов для вычисляемых здесь электростатической, дисперсионной и отталкивательной компонент адсорбционной энергии, ограничения, накладываемые при подсчете этих компонент ( жесткость кристаллической решетки адсорбента, неучет влияния соседей-молекул адсорбата, аддитивность дисперсионных сил и др.), так как это отвлекло бы нас от поставленной цели. [5]
Упрощая, эту аддитивность можно объяснить как результат согласованного ( в такт) движения электронных осцилляторов, которое понижает общую нулевую энергию системы. Аддитивность дисперсионных сил проявляется в адсорбции, в процессах, связанных с конденсацией газа и др. Дисперсионные силы играют большую роль при взаимодействии не только отдельных молекул, но и макроскопических частиц, например коллоидных. [6]
Дисперсионные силы играют большую роль при взаимодействии не только отдельных молекул, но и макроскопических частиц, например коллоидных. Благодаря аддитивности дисперсионных сил энергия взаимодействия однбй молекулы со всеми молекулами другой коллоидной частицы убывает уже не пропорционально шестой, а только третьей степени расстояния. [7]
Гельман [2] еще в 1937 г. показал, что на расстояниях, с которыми мы имеем дело в адсорбции, роль обменных эффектов ( первое приближение) становится весьма значительной. Теряется аддитивность дисперсионных сил. [8]
Силы Лондона - Ван-дер - Ваальса, возникающие между отдельными атомами, проявляются на очень малых расстояниях порядка атомных размеров. При взаимодействии коллоидных частиц вследствие аддитивности дисперсионных сил взаимодействие между частицами проявляется на значительно больших расстояниях. [9]
Они универсальны, так как существуют в любых системах, где имеются электроны. Результатом этого является аддитивность дисперсионных сил. Электроны одной молекулы могут учитывать положение электронов нескольких соседних молекул, что было бы, конечно, невозможно при движении электронов в такт. [10]
Если один из углов тупой, то в большинстве случаев величина 3 cos - [ 1 cos 72 cos y3 - - 1 будет меньше нуля и, следовательно, будет иметь место притяжение. Различные конфигурации молекул взаимно уничтожают или уменьшают отклонение от аддитивности. Расчеты, произведенные Аксильродом для плотно упакованных кристаллов Ne, Ar, Кг, Хе, Н2 и N2, показывают, что отклонение от аддитивности дисперсионных сил в общем не превышает нескольких ( - 5) процентов от общей энергии взаимодействия. В жидкостях и газах вследствие менее упорядоченного распределения молекул отклонение от аддитивности должно быть еще меньшим. [11]
Если один из углов тупой, то в большинстве случаев величина 3 cos - [ 1 cos y2 cos y3 1 будет меньше нуля и, следовательно, будет иметь место притяжение. Различные конфигурации молекул взаимно уничтожают или уменьшают отклонение от аддитивности. Расчеты, произведенные Аксильродом для плотно упакованных кристаллов Ne, Ar, Кг, Хе, И2 и N2, показывают, что отклонение от аддитивности дисперсионных сил в общем не превышает нескольких ( - - 5) процентов от общей энергии взаимодействия. В жидкостях и газах вследствие менее упорядоченного распределения молекул отклонение от аддитивности должно быть еще меньшим. Поэтому дисперсионные силы с достаточно. [12]
Уже в 1932 г. Кальман и Вильштеттер [51] указали на то, что благодаря суммированию межатомных взаимодействий силы притяжения макроскопических частиц должны быть существенно больше сил притяжения отдельных атомов или молекул. Могут быть предложены два пути для вычисления энергии взаимодействия конденсированных фаз. Лифшиц [54] избрал макроскопический способ рассмотрения, при котором не предполагается аддитивность дисперсионных сил, справедливая только для разреженного газа. Ренне и Ниибер [55] недавно установили, что с помощью микроскопической теории также могут быть получены результаты, согласующиеся с данными макроскопической теории, если неаддитивность учитывается введением соответствующих поправочных членов. В последнее время Лангбейном [56] на основе микроскопической теории и учета макроскопической экранировки флук-туационного поля выведено общее уравнение для энергии взаимодействия частиц. [13]
Расположение Ко и энергетических уровней определяется соотношением между энергией взаимодействия Я12 и энергиями начальных ионного и нейтрального состояний. При R0Ri основное состояние ближе к нейтральному, а при RoR оно становится ионным. Для возбужденных состояний действительны обратные соотношения. Кривая нейтрального состояния будет описывать изменение энергии дисперсионного взаимодействия двух соседних молекул в кристалле, что справедливо благодаря аддитивности дисперсионных сил. [14]
Мы рассмотрели кратко две теории адсорбции - теорию мономолекулярной адсорбции Ленгмюра и теорию полимолекулярной адсорбции Поляни, на первый взгляд исключающие друг друга. Возникает вопрос, какая из этих теорий более правильна. На это следует ответить, что обе теории ограничены в применении. Теория Поляни применима только к явлениям чисто физической адсорбции. Однако теория Ленгмюра не может быть применена для объяснения адсорбции на тонкопористых адсорбентах, имеющих сужающиеся поры. В местах сужения, вследствие аддитивности дисперсионных сил, адсорбционный потенциал более высок и в таких местах происходит более интенсивная адсорбция. [15]
Страницы: 1 2