Адекватность - выбранная модель
Cтраница 1
Адекватность выбранной модели устанавливается по критерию Фишера. [1]
Адекватность выбранной модели реальному производственному процессу во многом зависит от критериев единой подотраслевой классификации продукции и ресурсов, а также их взаимосвязей в виде взаимозаменяемости. [2]
Далее определим значимость коэффициентов по - критерию и адекватность выбранной модели по критерию Фишера. [3]
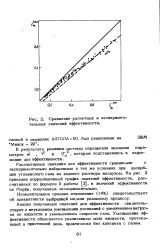 |
Сравнение расчетных и экспериментальных значений эффективности. [4] |
Незначительное среднее отклонение ( 14 %) свидетельствует об адекватности выбранной модели реальному процессу. [5]
Разные значения времени запаздывания, полученные по двум методам, свидетельствуют о недостаточной адекватности выбранных моделей действительным процессам, что, очевидно, обусловлено сложностью этих процессов. [6]
 |
Экспериментальные константы равновесия для трех неорганических полимерных систем. [7] |
Следовательно, kt совпадают с константами равновесия некоторых обменных реакций из схемы (4.123), а независимость их значений от средней молекулярной массы полимера [44-45] свидетельствует об адекватности выбранной модели. [8]
Для того чтобы уточнить понятие наилучшим образом, исследователь должен формализовать задачу, выбрать модель. Очевидно, мера адекватности выбранной модели и изучаемой действительности является решающим фактором, определяющим эффективность и действенность используемых затем методов статистической обработки. [9]
Из приведенных примеров видно, что хотя определение ЭР из констант равновесия строится на экспериментальной основе, оно не свободно от упрощений, несущих в себе элемент неопределенности. Главными из них являются предположения об адекватности выбранной модели гипотетической молекуле исследуемого соединения с локализованными связями и об одинаковости изменений энергий а-связей и энергий сольватации для ароматического соединения и неароматической модели в изучаемой реакции. Кроме того, метод требует оценки энергии л-сопряжения в модельном соединении независимым путем. [10]
После выбора типовой модели ( или комбинации нескольких) для описания исследуемого процесса ( условно разделенного на ряд звеньев) и принятия системы допущений для упрощения и обоснования принятой структурной схемы, а также для решения системы составленных дифференциальных уравнений, разрабатывается определенный моделирующий алгоритм, пользуясь которым и составляют программу для ЭВМ. Если математическое описание процесса представляет собой сложную систему конечных и дифференциальных уравнений, то от возможности построения достаточно надежного моделирующего алгоритма зависит применимость математической модели. В соответствии с составленной программой машина последовательно выполняет опеоа-ции, дающие информацию о ходе процесса и конечных его результатах. Следующий этап моделирования с помощью аналоговой или цифровой вычислительной машины состоит в проверке адекватности выбранной модели исследуемому процессу или аппарату и ее коррекции. [11]
Измеряемые координаты технических систем представляют собой в общем случае комбинацию нестационарного полезного сигнала и стационарной помехи. Упрощенная аппроксимация таких процессов полиномами заданного порядка возможна лишь в сравнительно узких интервалах времени, длина которых, как правило, заранее неизвестна и должна определяться на основе тех же измерений, которые используются для оценивания состояния системы. Степень аппроксимирующего полинома также не может быть выбрана априорно, она подбирается путем анализа этих же измерений. Таким образом, при использовании метода наименьших квадратов для оценивания состояния систем наряду с непосредственным оцениванием координат этих систем необходимо решать ряд задач проверки адекватности выбранной модели измеряемому процессу. [12]
Страницы: 1