Фазовая анизотропия
Cтраница 1
Фазовая анизотропия характеризуется тем, что оптический путь лучей света для двух ортогональных поляризаций при прохождении через элемент ( отражении от него) становится различным. [1]
Для всех резонаторов с чисто фазовой анизотропией расчет методом матриц Джонса не дает разницы в потерях для собственных поляризаций. [2]
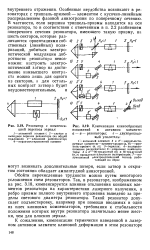 |
Резонатор с компенса - [ IMAGE ] Компенсация клинообразных. [3] |
Особенные неудобства возникают в резонаторах с триппель-призмой - элементом с кусочно-линейным распределением фазовой анизотропии по поперечному сечению. [4]
 |
Обход резонатора при матрич - ДИТ К появлению еще ОДНОГО. [5] |
Вещественная часть Я ь Я 2 дает величину потерь, связанных с амплитудной анизотропией совокупности элементов резонатора; мнимая часть Я ь Я 2 определяет зависящий от фазовой анизотропии набег фазы для данной собственной поляризации. [6]
Состояние поляризации собственной волны восстанавливается в любом поперечном сечении резонатора после циклического обхода. Существование определенных собственных состояний поляризации резонатора связано с наличием амплитудной или фазовой анизотропии образующих резонатор элементов. Обычно резонатор имеет два собственных состояния поляризации, которые характерны для всей системы собственных типо в колебаний ( см. гл. [7]
Неодимовое стекло является изотропным материалом, и поэтому в нем возможно генерировать или усиливать излучение с любой поляризацией. Такой режим работы характерен для лазеров однократного действия при невысоких мощностях тепловыделения. С другой стороны, с повышением мощности тепловыделения в неодимовом стекле наводятся термонапряжения, превращающие активный элемент в фазовую пластинку, изменяющую поляризацию излучения ( см. гл. При этом из-за низкой теплопроводности стекла и возникающих вследствие этого больших перепадов температуры фазовая анизотропия может быть достаточно велика, что сильно сказывается на работе как генераторов, так и усилителей поляризованного излучения. [8]
Собственные векторы матрицы являются векторами Джонса состояний поляризации, не изменяющихся при прохождении рассматриваемого оптического элемента. Собственные значения в общем случае комплексны. Модуль собственного значения матрицы М при указанной нормировке (7.9) определяет амплитудное пропускание, а аргумент - фазовый набег. Оптический элемент обладает невырожденной амплитудной анизотропией, если модули собственных значений матрицы М различны. Неравенство аргументов собственных значений характеризует фазовую анизотропию оптического элемента. [9]
Страницы: 1